2D Physik für Spiele
Übersicht BlitzBasic
BlitzBasic  FAQ und Tutorials
FAQ und Tutorials|
|
NoobodyBetreff: 2D Physik für Spiele |
Antworten mit Zitat |
|---|---|---|
|
Wer schon mal versucht hat, eine Physikengine für seine Spiele zu schreiben, kennt das sicher: Man hat ja in der Schule schön die Formeln gelernt für alle möglichen Bereiche der Kinetik, also warum nicht auch für das eigene Spiel verwenden?
Ich selbst habe einige Male diesen Ansatz probiert, bin aber kläglichst gescheitert - es schien mir unmöglich, alle beteiligten Kräfte zu berücksichtigen. Nun bin ich aber vor kurzem auf einen Artikel über die Physik in 'Hitman: Codename 47' gestossen, welche einen andere Herangehensweise benutzt. Sie ist schnell, stabil und relativ einfach zu implementieren - man kann ihr sogar vorgeben, wie genau die Physik berechnet werden soll (und somit wie rechenintensiv sie ist), wenn man je nach Szene die Rechenzeit für andere Dinge braucht. Weil ich das sehr interessant fand, dachte ich, ich schreibe ein Tutorial dazu. In diesem Tutorial werde ich die sogenannte Verletphysik vorstellen und eine kleine Implementation in BB zeigen - bevor wir nun aber ans Programmieren gehen, muss ein wenig Theorie vorweggenommen werden. Wie ist eigentlich so ein Physikobjekt aufgebaut? In der Realität ist das klar, da besteht jeder Körper aus Teilchen, die sich gegenseitig abstossen und anziehen, wodurch die Physik massgeblich bestimmt wird. Am Computer können wir das kaum auch so machen - man stelle sich vor, wie viel Rechenaufwand es bräuchte, um tausende von Teilchen auf Kollision zu prüfen! Nein, unser Ansatz wird sein, dass ein Körper aus wenigen Partikeln besteht, die untereinander mit Federn verbunden sind. Diese Federn haben theoretisch eine unendliche Federkraft, sprich, sie lassen sich überhaupt nicht zusammenstossen oder auseinanderziehen. Dass das nur theoretisch so ist und in der Praxis anders aussehen wird, sehen wir dann später. 
Bevor wir uns die Federn vornehmen, betrachten wir mal die Partikel. Sie haben sicher einmal eine Position (X|Y), eine Geschwindigkeit und eine Beschleunigung. Würde man ein solches Partikel aktualisieren wollen, würde das nach herkömmlicher Herangehensweise so aussehen: Code: [AUSKLAPPEN] X = X + VX*DT
Y = Y + VY*DT VX = VX + AX*DT VY = VY + AY*DT Hier stehen X und Y für die Position, VX und VY für die Geschwindigkeit, AX und AY für die Beschleunigung und DT für die vergangene Zeitspanne (so kann man die Physik schneller/langsamer laufen lassen oder das ganze Frameunabhängig programmieren). Nach der Verlet - Herangehensweise machen wir das aber anders. Wir berechnen nämlich die Geschwindigkeit aus der alten und der aktuellen Position. Das hat den Vorteil, dass das ganze relativ stabil läuft - bei Kollisionen etc. müssen wir nur die aktuelle Position verändern, die Geschwindigkeit passt sich von selbst an. Zum aktualisieren sieht das ganze also jetzt so aus: Code: [AUSKLAPPEN] X = X + (X - OldX ) + AX*DT^2*1/2
Y = Y + (Y - OldY ) + AY*DT^2*1/2 Der Teil "(X - OldX)" berechnet die Geschwindigkeit aus der aktuellen Position und der Position im letzten Frame; "AX*DT^2" ist eine Formel, um die Beschleunigung direkt in zurückgelegten Weg umzurechnen (so haben wir alles in einer Zeile erledigt). Ein so ausgelegtes Partikel braucht also Variablen, die seine aktuelle und seine alte Position festlegen und Variablen für die Beschleunigung - das genügt bereits. Jetzt haben wir also die Partikel festgelegt und haben eine Funktion zum Aktualisieren - setzen wir das doch erstmal um in Code: [AUSKLAPPEN] Const GWIDTH = 800 ;Grafikzeugs und so
Const GHEIGHT = 600 Graphics GWIDTH, GHEIGHT, 0, 2 SetBuffer BackBuffer() Type TParticle Field X# ;Position Field Y# Field OldX# ;Alte Position Field OldY# Field A_X# ;Beschleunigung Field A_Y# End Type Const GRAVITY_X# = 0 ;Unsere Gravitation Const GRAVITY_Y# = 1 Const TIMESTEP# = 1 ;Die Zeit, die pro Aktualisierung vergeht - spielt damit rum, um SlowMo bzw. Zeitraffer zu erreichen Timer = CreateTimer( 60 ) ;Wir wollen ja schliesslich keine 100% Auslastung. CreateParticle( 200, 200 ) While Not KeyHit( 1 ) Cls UpdateForces() UpdateVerlet() UpdateConstraints() Render() Flip 0 WaitTimer Timer Wend End Function UpdateForces() For Particle.TParticle = Each TParticle Particle\A_X# = GRAVITY_X# ;Gravitationskraft anwenden Particle\A_Y# = GRAVITY_Y# Next End Function Function UpdateVerlet() For Particle.TParticle = Each TParticle OldX# = Particle\X# ;Aktuelle Werte zwischenspeichern OldY# = Particle\Y# Particle\X# = 2*Particle\X# - Particle\OldX# + Particle\A_X#*TIMESTEP#*TIMESTEP#*0.5 ;Neue Position berechnen Particle\Y# = 2*Particle\Y# - Particle\OldY# + Particle\A_Y#*TIMESTEP#*TIMESTEP#*0.5 Particle\OldX# = OldX# ;Alte Werte ablegen Particle\OldY# = OldY# Next End Function Function UpdateConstraints() ;Hier würden die Federn aktualisiert - wir haben aber noch keine, darum ist hier nichts. End Function Function Render() ;Hier zeichnen wir das ganze - Lockbuffer & WritePixelFast für mehr Geschwindigkeit LockBuffer BackBuffer() For Particle.TParticle = Each TParticle If Particle\X# >= 0 And Particle\X# < GWIDTH Then If Particle\Y# >= 0 And Particle\Y# < GHEIGHT Then WritePixelFast Floor( Particle\X# ), Floor( Particle\Y# ), $00FFFFFF EndIf EndIf Next UnlockBuffer BackBuffer() End Function Function CreateParticle.TParticle( X#, Y# ) ;Diese Funktion erstellt ein Partikel und liefert es zurück Particle.TParticle = New TParticle Particle\X# = X# Particle\Y# = Y# Particle\OldX# = X# Particle\OldY# = Y# Return Particle End Function Wenn man jetzt diesen Code ausführt, passiert nichts besonderes - ein weisser Punkt fällt nach unten. Aber mit diesem Code haben wir bereits ein wesentliches Grundgerüst für spätere Erweiterungen. Jetzt fehlt aber noch ein wesentlicher Bestandteil - die Federn! Dafür brauchen wir wieder etwas Theorie. Eine Feder besteht immer aus zwei Partikeln, die immer den gleichen Abstand voneinander haben sollen (die Feder hat ja eine unendliche Kraft, sprich sie lässt sich weder auseinanderziehen noch zusammendrücken). Also müssen wir nun jedes Frame den Abstand der beiden Partikel messen und ihre Positionen korrigieren, wenn etwas nicht stimmt. Die Berechnung dafür sieht folgendermassen aus: Code: [AUSKLAPPEN] DeltaX = X2 - X1
DeltaY = Y2 - Y1 DeltaLength = Sqr( DeltaX*DeltaX + DeltaY*DeltaY ) Difference = ( DeltaLength - SpringLength )/DeltaLength X1 = X1 + DeltaX*Difference/2 Y1 = Y1 + DeltaY*Difference/2 X2 = X2 - DeltaX*Difference/2 Y2 = Y2 - DeltaY*Difference/2 Das funktioniert also wie folgt: Zuerst rechnen wir den Vektor vom einen Punkt (X1) zum anderen Punkt (X2) aus. Dann berechnen wir den Betrag des Vektors (sprich seine Länge) und schliesslich die Differenz zwischen der aktuellen Länge und der eigentlichen Länge der Feder im ungestauchten Zustand. Die beiden Punkte werden dann einfach in Richtung des anfangs ausgerechneten Vektors um die Differenz verschoben - schon stimmt ihr Abstand wieder. Aber Moment mal, was ist, wenn der eine Punkt nun gleichzeitig noch zu einer anderen Feder gehört? 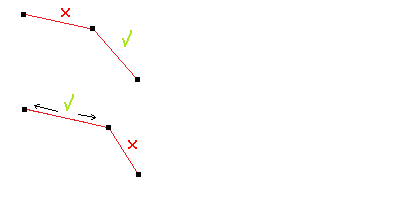
Im Bild sehen wir, dass vor der Korrektur die eine Feder die richtige Länge hat, die andere jedoch (z.B. durch Kollision o.ä.) zusammengedrückt ist. Dass wir dies korrigieren müssen, ist klar, schliesslich darf die Feder ja eigentlich nicht zusammengedrückt werden. Also schieben wir die Eckpunkte entlang des Vektors auseinander - aber was sehen wir denn da? Jetzt ist die andere Feder, die vorher korrekt war, zusammengedrückt! Hier kommt der am Anfang angesprochene Genauigkeitsfaktor ins Spiel. Wenn wir nun die Federn auf dem Bild im gleichen Frame ein zweites Mal aktualisieren würden, wäre wieder die eine Feder richtig und die andere zusammengedrückt - jedoch nicht mehr so stark wie vor dem ersten Durchgang. Je öfter wir also die Federn neu berechnen, desto näher kommen wir an den Punkt, an dem keine der Federn gestaucht ist. Das heisst für uns nun, dass, wenn man im Spiel noch ein gutes Stück Rechenzeit übrig hat, man die Funktion einige dutzend Male laufen lässt, bei Engpässen kann man sie auch nur einmal ausführen; jedoch muss man dann mit Einbussen bezüglich Realismus rechnen. So, jetzt aber genug Theorie - machen wir uns an die Umsetzung. Eine Feder besteht aus jeweils zwei Partikeln, also sollte der entsprechende Type auch zwei Partikel aufnehmen können. In der vorhin leeren 'UpdateConstraints' - Funktion können wir nun die vorgestellten Berechnungen unterbringen. Ausserdem können wir dort gleich überprüfen, ob einer der Partikel einer Feder aus dem Bildschirm geschoben wurde (entweder durch das korrigieren einer Feder oder durch die Gravitation). Der Beispielcode sieht nun also so aus: Code: [AUSKLAPPEN] Const GWIDTH = 800 ;Grafikzeugs und so
Const GHEIGHT = 600 Graphics GWIDTH, GHEIGHT, 0, 2 SetBuffer BackBuffer() Type TParticle Field X# ;Position Field Y# Field OldX# ;Alte Position Field OldY# Field A_X# ;Beschleunigung Field A_Y# End Type Type TConstraint Field P1.TParticle ;Die beiden Eckpunkte Field P2.TParticle Field Length# ;Die Länge der Feder End Type Const GRAVITY_X# = 0 ;Unsere Gravitation Const GRAVITY_Y# = 1 Const TIMESTEP# = 1 ;Die Zeit, die pro Aktualisierng vergeht - spielt damit rum, um SlowMo bzw. Zeitraffer zu erreichen Global Iterations = 10 ;Anzahl Durchläufe Timer = CreateTimer( 60 ) ;Wir wollen ja schliesslich keine 100% Auslastung. Vertex1.TParticle = CreateParticle( 190, 220 ) ;Das Testdreieck erstellen Vertex2.TParticle = CreateParticle( 260, 210 ) Vertex3.TParticle = CreateParticle( 230, 260 ) CreateConstraint( Vertex1, Vertex2 ) CreateConstraint( Vertex2, Vertex3 ) CreateConstraint( Vertex3, Vertex1 ) While Not KeyHit( 1 ) Cls UpdateForces() UpdateVerlet() UpdateConstraints() Render() ;Folgende Zeilen auskommentieren, um das Dreick fliegen zu lassen ;Vertex1\X# = MouseX() ;Vertex1\Y# = MouseY() Flip 0 WaitTimer Timer Wend End Function UpdateForces() For Particle.TParticle = Each TParticle Particle\A_X# = GRAVITY_X# ;Gravitationskraft anwenden Particle\A_Y# = GRAVITY_Y# Next End Function Function UpdateVerlet() For Particle.TParticle = Each TParticle OldX# = Particle\X# ;Aktuelle Werte zwischenspeichern OldY# = Particle\Y# Particle\X# = 2*Particle\X# - Particle\OldX# + Particle\A_X#*TIMESTEP#*TIMESTEP#*0.5 ;Neue Position berechnen Particle\Y# = 2*Particle\Y# - Particle\OldY# + Particle\A_Y#*TIMESTEP#*TIMESTEP#*0.5 Particle\OldX# = OldX# ;Alte Werte ablegen Particle\OldY# = OldY# Next End Function Function UpdateConstraints() For i = 1 To Iterations For Particle.TParticle = Each TParticle ;Partikel wieder in den Bildschirm schieben Particle\X# = Min( Max( Particle\X#, 0 ), GWIDTH - 1 ) Particle\Y# = Min( Max( Particle\Y#, 0 ), GHEIGHT - 1 ) Next For Constraint.TConstraint = Each TConstraint ;Federn wie erklärt aktualisieren DeltaX# = Constraint\P2\X# - Constraint\P1\X# DeltaY# = Constraint\P2\Y# - Constraint\P1\Y# DeltaLength# = Sqr( DeltaX#*DeltaX# + DeltaY#*DeltaY# ) Diff# = ( DeltaLength# - Constraint\Length# )/DeltaLength# Constraint\P1\X# = Constraint\P1\X# + DeltaX#*0.5*Diff# Constraint\P1\Y# = Constraint\P1\Y# + DeltaY#*0.5*Diff# Constraint\P2\X# = Constraint\P2\X# - DeltaX#*0.5*Diff# Constraint\P2\Y# = Constraint\P2\Y# - DeltaY#*0.5*Diff# Next Next End Function Function Render() ;Hier zeichnen wir das ganze - Lockbuffer & WritePixelFast für mehr Geschwindigkeit LockBuffer BackBuffer() Color 255, 0, 0 ;Alle Federn... For Constraint.TConstraint = Each TConstraint Line Constraint\P1\X#, Constraint\P1\Y#, Constraint\P2\X#, Constraint\P2\Y# Next For Particle.TParticle = Each TParticle ;... und Partikel zeichnen If Particle\X# >= 0 And Particle\X# < GWIDTH Then If Particle\Y# >= 0 And Particle\Y# < GHEIGHT Then WritePixelFast Floor( Particle\X# ), Floor( Particle\Y# ), $00FFFFFF EndIf EndIf Next UnlockBuffer BackBuffer() End Function Function CreateParticle.TParticle( X#, Y# ) ;Diese Funktion erstellt ein Partikel und liefert es zurück Particle.TParticle = New TParticle Particle\X# = X# Particle\Y# = Y# Particle\OldX# = X# Particle\OldY# = Y# Return Particle End Function Function CreateConstraint.TConstraint( P1.TParticle, P2.TParticle ) ;Diese Funktion erstellt eine Feder und liefert sie zurück If P1 <> P2 Then ;Wenn eine Feder zwischen dem gleichen Partikel gespannt versucht wird, gibt das unschöne Auswirkungen Constraint.TConstraint = New TConstraint Constraint\P1 = P1 Constraint\P2 = P2 ;Die Länge ausrechnen (leider recht lange geworden, sorry) Constraint\Length# = Sqr( ( Constraint\P1\X# - Constraint\P2\X# )*( Constraint\P1\X# - Constraint\P2\X# ) + ( Constraint\P1\Y# - Constraint\P2\Y# )*( Constraint\P1\Y# - Constraint\P2\Y# ) ) Return Constraint EndIf End Function Function Min#( A#, B# ) ;Minimum aus zwei Werten zurückliefern If A# < B# Then Return A# Else Return B# End Function Function Max#( A#, B# ) ;Maximum aus zwei Werten zurückliefern If A# > B# Then Return A# Else Return B# End Function Obwohl wir Drehmoment etc. überhaupt nicht beachtet haben, kommt das dank Verlet ganz von alleine. Ich bin jetzt am Ende dieses Teils des Tutorials - ich hoffe, ich konnte mich einigermassen verständlich ausdrücken. Wie wir jetzt gesehen haben, ist 2D - Physik keine grosse Sache (zumindest bis zum dem Punkt, wo wir jetzt sind). Mithilfe des Partikel - Federmodells können nahezu alle Körper simuliert werden und nicht nur ein Dreieck wie im Beispielprogramm. Hier habe ich nun noch ein Stück Code, mit dem man per Maus und Tastatur beliebige Polygone erstellen kann - wenn man ein wenig damit rumspielt, sieht man relativ schnell, wie gut die Physik trotz ihrer simplen Implementierung aussieht - perfekt für Spiele! Code: [AUSKLAPPEN] Const GWIDTH = 800 ;Grafikzeugs und so
Const GHEIGHT = 600 Graphics GWIDTH, GHEIGHT, 0, 2 SetBuffer BackBuffer() Type TParticle Field X# ;Position Field Y# Field OldX# ;Alte Position Field OldY# Field A_X# ;Beschleunigung Field A_Y# End Type Type TConstraint Field P1.TParticle ;Die beiden Eckpunkte Field P2.TParticle Field Length# ;Die Länge der Feder End Type Const GRAVITY_X# = 0 ;Unsere Gravitation Const GRAVITY_Y# = 1 Const TIMESTEP# = 1 ;Die Zeit, die pro Aktualisierng vergeht - spielt damit rum, um SlowMo bzw. Zeitraffer zu erreichen Global Iterations = 10 ;Anzahl Durchläufe Global GameRunning Global SelectedParticle.TParticle Global SelectedConstraint.TConstraint Global SetConstraint Global FollowParticle.TParticle Timer = CreateTimer( 60 ) ;Wir wollen ja schliesslich keine 100% Auslastung. While Not KeyHit( 1 ) Cls UserInput() If GameRunning Then UpdateForces() UpdateVerlet() UpdateConstraints() EndIf Render() Color 128, 128, 128 Text 0, 0, "Leertaste zum starten/pausieren der Simulation. Enter, um Partikel durch die Gegend zu ziehen." Text 0, 15, "Linke Maustaste für neues Partikel, rechte Maustaste für neue Feder" Flip 0 WaitTimer Timer Wend End Function UpdateForces() For Particle.TParticle = Each TParticle Particle\A_X# = GRAVITY_X# ;Gravitationskraft anwenden Particle\A_Y# = GRAVITY_Y# Next End Function Function UpdateVerlet() For Particle.TParticle = Each TParticle OldX# = Particle\X# ;Aktuelle Werte zwischenspeichern OldY# = Particle\Y# Particle\X# = 2*Particle\X# - Particle\OldX# + Particle\A_X#*TIMESTEP#*TIMESTEP#*0.5 ;Neue Position berechnen Particle\Y# = 2*Particle\Y# - Particle\OldY# + Particle\A_Y#*TIMESTEP#*TIMESTEP#*0.5 Particle\OldX# = OldX# ;Alte Werte ablegen Particle\OldY# = OldY# Next End Function Function UpdateConstraints() For i = 1 To Iterations For Particle.TParticle = Each TParticle ;Partikel wieder in den Bildschirm schieben Particle\X# = Min( Max( Particle\X#, 0 ), GWIDTH - 1 ) Particle\Y# = Min( Max( Particle\Y#, 0 ), GHEIGHT - 1 ) Next For Constraint.TConstraint = Each TConstraint ;Federn wie erklärt aktualisieren DeltaX# = Constraint\P2\X# - Constraint\P1\X# DeltaY# = Constraint\P2\Y# - Constraint\P1\Y# DeltaLength# = Sqr( DeltaX#*DeltaX# + DeltaY#*DeltaY# ) Diff# = ( DeltaLength# - Constraint\Length# )/DeltaLength# Constraint\P1\X# = Constraint\P1\X# + DeltaX#*0.5*Diff# Constraint\P1\Y# = Constraint\P1\Y# + DeltaY#*0.5*Diff# Constraint\P2\X# = Constraint\P2\X# - DeltaX#*0.5*Diff# Constraint\P2\Y# = Constraint\P2\Y# - DeltaY#*0.5*Diff# Next If FollowParticle <> Null Then FollowParticle\X# = MouseX() FollowParticle\Y# = MouseY() EndIf Next End Function Function Render() ;Hier zeichnen wir das ganze - Lockbuffer & WritePixelFast für mehr Geschwindigkeit LockBuffer BackBuffer() Color 255, 0, 0 ;Alle Federn... For Constraint.TConstraint = Each TConstraint Line Constraint\P1\X#, Constraint\P1\Y#, Constraint\P2\X#, Constraint\P2\Y# Next For Particle.TParticle = Each TParticle ;... und Partikel zeichnen If Particle\X# >= 0 And Particle\X# < GWIDTH Then If Particle\Y# >= 0 And Particle\Y# < GHEIGHT Then WritePixelFast Floor( Particle\X# ), Floor( Particle\Y# ), $00FFFFFF EndIf EndIf Next UnlockBuffer BackBuffer() End Function Function CreateParticle.TParticle( X#, Y# ) ;Diese Funktion erstellt ein Partikel und liefert es zurück Particle.TParticle = New TParticle Particle\X# = X# Particle\Y# = Y# Particle\OldX# = X# Particle\OldY# = Y# Return Particle End Function Function CreateConstraint.TConstraint( P1.TParticle, P2.TParticle ) ;Diese Funktion erstellt eine Feder und liefert sie zurück If P1 <> P2 Then ;Wenn eine Feder zwischen dem gleichen Partikel gespannt versucht wird, gibt das unschöne Auswirkungen Constraint.TConstraint = New TConstraint Constraint\P1 = P1 Constraint\P2 = P2 ;Die Länge ausrechnen (leider recht lange geworden, sorry) Constraint\Length# = Sqr( ( Constraint\P1\X# - Constraint\P2\X# )*( Constraint\P1\X# - Constraint\P2\X# ) + ( Constraint\P1\Y# - Constraint\P2\Y# )*( Constraint\P1\Y# - Constraint\P2\Y# ) ) Return Constraint EndIf End Function Function Min#( A#, B# ) ;Minimum aus zwei Werten zurückliefern If A# < B# Then Return A# Else Return B# End Function Function Max#( A#, B# ) ;Maximum aus zwei Werten zurückliefern If A# > B# Then Return A# Else Return B# End Function Function UserInput() ;Der ganze Kram zum Kontrollieren der Simulation durch User If MouseHit( 1 ) Then CreateParticle( MouseX(), MouseY() ) If MouseHit( 2 ) Then SetConstraint = ( SetConstraint + 1 ) Mod 2 MX = MouseX() MY = MouseY() Local NearestParticle.TParticle, NearestDistance# = 100000 For Particle.TParticle = Each TParticle Dist# = ( Particle\X# - MX )*( Particle\X# - MX ) + ( Particle\Y# - MY )*( Particle\Y# - MY ) If Dist# < NearestDistance# Then NearestDistance# = Dist# NearestParticle = Particle EndIf Next If Not SetConstraint Then CreateConstraint( SelectedParticle, NearestParticle ) Else SelectedParticle = NearestParticle EndIf EndIf If KeyHit( 28 ) Then If FollowParticle = Null Then MX = MouseX() MY = MouseY() NearestDistance# = 100000 For Particle.TParticle = Each TParticle Dist# = ( Particle\X# - MX )*( Particle\X# - MX ) + ( Particle\Y# - MY )*( Particle\Y# - MY ) If Dist# < NearestDistance# Then NearestDistance# = Dist# NearestParticle = Particle EndIf Next FollowParticle = NearestParticle Else FollowParticle = Null EndIf EndIf If SetConstraint = 1 Then Line SelectedParticle\X#, SelectedParticle\Y#, MouseX(), MouseY() If KeyHit( 57 ) Then GameRunning = Not GameRunning End Function Im nächsten Teil (falls es einen gibt) werde ich die Kollision von Physikobjekten untereinander ansprechen, was ein wenig komplizierter wird (ich selbst habe auch noch nicht eine hundertprotzentig stabile Lösung gefunden). Danke für euer Interesse. |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
- Zuletzt bearbeitet von Noobody am Di, Jan 13, 2009 15:42, insgesamt einmal bearbeitet
|
|
hecticSieger des IS Talentwettbewerb 2006 |
Antworten mit Zitat |
|---|---|---|
|
Ich finde es garnicht schlecht. Da ich sowas auch hemacht habe, finde ich besonders die Funktion UserInput interessant, weil man ins laufende Geschehen eingreifen kann.
Nur so als Info/Tipps: - Soweit ich weiß, kann man über eine Verlet-Integration keine absolut starren Körper bilden. Das geht spätestens dann schief, wenn man Kollision einbaut (was bei deinem Code schon die Aussenwände sind). Man könnte dem nur mit erheblichen Mehraufwand entgegentretten. Daher gilt es das ganze möglichst stabil zu machen bei möglichst wenig Rechenaufwand und Programmloops. Stabilität kann man zum Beispiel durch Übersteuerung erreichen, was aber in seltenen Fällen zur ''Sprengung'' der Struktur führen kann. - Ein alleiniges WritePixel ist ein klein wenig schneller als WritePixelFast + eingener Überprüfung ob ein Pixel innerhalb des Bildschirmes ist. Da der Unterschied von beiden Befehlen der ist, das Blitz die Überprüfung eben selbst übernimmt. - Falls es dir gelingt, könntest du eine schnelle Möglichkeit finden, wie man Fehlberechnungen übergehen kann. Zum Beispiel tretten Fehlberechnungen dann auf, wenn bestimmte Verbindungen überbeansprucht wurden und dadurch in ständiger Spannung stehen. Man kann das auch einfach selbst simulieren, indem man folgenden Code in dein Mainloop mit rein packt. Mit den Tasten [1] und [2] kann man dann die ersterstellte Verbindung dessen Länge manipulieren. Wenn bei einer Änderung der Länge andere Längen in wiederruf stehen, dreht sich auf einmal der ganze Körper. Das Problem tritt auch bei meiner Physix -Funktionssammlung auf. Meiner Meinung nach könnte man dem entgegentretten wenn man die Funktion für Verbindungenkorrekturen jedes zweite Frame rückwärts berechnet. Also zuerst 1, 2, 3, 4... und dann ... 4, 3, 2, 1 etc... Sicher bin ich mir denoch nicht. Code: [AUSKLAPPEN] If KeyDown(2) Then
Constraint.TConstraint = First TConstraint Constraint\Length=Constraint\Length+0.5 End If If KeyDown(3) Then Constraint.TConstraint = First TConstraint Constraint\Length=Constraint\Length-0.5 End If |
||
| Download der Draw3D2 V.1.1 für schnelle Echtzeiteffekte über Blitz3D | ||
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
Hi hectic,
Erstmal danke für dein Feedback. Das mit den starren Körpern ist mir bewusst, deswegen schrieb ich noch hin, dass die Federn nur in der Theorie unendlich stark (=starr) sind, dass das in der Praxis aber anders aussieht (ich glaube zumindest das war das, was du meintest). Danke noch für den Tipp mit dem WritePixel, das war mir gar nicht bewusst, obwohl es eigentlich logisch ist. Zu den Verbindungen: Das ist mir auch schon aufgefallen, wenn die Physikobjekte durch eine Kollision mit hoher Geschwindigkeit extrem zusammengestaucht wurden. Bei einzelnen Dreiecken kommt das nicht vor, bei anderen Primitiven (zum Beispiel einer Box) geschieht das aber relativ schnell. Mal schauen, ob sich das irgendwie beheben lässt, aber ein solcher Fall tritt eigentlich äusserst selten auf - die Länge sollte man später einfach nicht mehr verändern und starke Kollisionen vermeiden. |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
|
|
peacemaker |
Antworten mit Zitat |
|---|---|---|
|
Ein wirklich cooles Tutorial, hätt ich atm mehr Zeit, würd ichs sofort ausprobieren, habe mich vor npaar Jahren auch versucht an ner Physik-Engine abzumühen. |
||
|
~Tehadon~
www.tehadon.de http://www.blitzforum.de/worklogs/14/ |
||
|
|
ToeB |
Antworten mit Zitat |
|---|---|---|
|
Cool sowas habe ich schon lange gesucht !
Aber wie prüft man die Kollision ? mfg ToeB |
||
|
Religiöse Kriege sind Streitigkeiten erwachsener Männer darum, wer den besten imaginären Freund hat.
Race-Project - Das Rennspiel der etwas anderen Art SimpleUDP3.0 - Neuste Version der Netzwerk-Bibliothek Vielen Dank an dieser Stelle nochmal an Pummelie, welcher mir einen Teil seines VServers für das Betreiben meines Masterservers zur verfügung stellt! |
||
|
|
hecticSieger des IS Talentwettbewerb 2006 |
Antworten mit Zitat |
|---|---|---|
|
Mit Blitz3D kann man für jeden TParticle ein Pivot mit eigenem Entitiyradius erstellen. Die Kollisionsflächen werden dann mit Triangles erstellt. Den Rest macht dann Blitz3D fast von alleine. Unter reinem 2D ist es schwiriger, da man jede Bewegung jedes TParticle mit einer Linienkollision jeder Linie im Raum vergleichen muß, was die Sache sehr langsam macht.
Eine einfache Bildschirmrandkollision ist allerdings ja bereits jetzt vorhanden. |
||
| Download der Draw3D2 V.1.1 für schnelle Echtzeiteffekte über Blitz3D | ||
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
Kollision folgt wie gesagt in einem nächsten Tutorial, an dem ich momentan noch arbeite.
Die interne Blitz - Kollision ist hierfür leider nur bedingt anwendbar - man kann nur bewegende mit statischen Objekten kollidieren lassen, für Kollision zwischen zwei bewegenden Objekten ist sie ungeeignet. Ich arbeite darum an einem Ansatz mithilfe der 'Seperating axis method', welcher noch nicht ganz rund funktioniert - aber es kommt noch, irgendwann. |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
|
|
aMulSieger des Minimalist Compo 01/13 |
Antworten mit Zitat |
|---|---|---|
|
hectic hat Folgendes geschrieben: Unter reinem 2D ist es schwiriger, da man jede Bewegung jedes TParticle mit einer Linienkollision jeder Linie im Raum vergleichen muß, was die Sache sehr langsam macht.
Muss man nicht einfach nur jedes Mal überprüfen ob die zwei Strecken sich schneiden? Das sollte doch nicht so schwer sein. Einfach die Gleichungen der Geraden aufstellen, Schnittpunkt bestimmen, schauen ob der Schnittpunkt im Intervall der Strecken liegt, fertig. Man kann das ganze sicher auch irgendwie mit Vektor-Kram machen, aber damit kenne ich mich nicht aus. @Nobody: Klasse Tutorial! (Hab es erst heute bemerkt.) |
||
|
Panic Pong - ultimate action mashup of Pong and Breakout <= aktives Spiele-Projekt, Downloads mit vielen bunten Farben!
advASCIIdraw - the advanced ASCII art program <= aktives nicht-Spiele-Projekt, must-have für ASCII/roguelike/dungeon-crawler fans! Alter BB-Kram: ThroughTheAsteroidBelt - mit Quelltext! | RGB-Palette in 32²-Textur / Farbige Beleuchtung mit Dot3 | Stereoskopie in Blitz3D | Teleport-Animation Screensaver |
||
|
|
hecticSieger des IS Talentwettbewerb 2006 |
Antworten mit Zitat |
|---|---|---|
|
Ja! Ich schrieb ja:
''Unter reinem 2D ist es schwiriger, da man jede Bewegung jedes TParticle mit einer Linienkollision jeder Linie im Raum vergleichen muß, was die Sache sehr langsam macht.''. Vielleicht nur etwas umständlich in Worte gefasst. |
||
| Download der Draw3D2 V.1.1 für schnelle Echtzeiteffekte über Blitz3D | ||
|
|
aMulSieger des Minimalist Compo 01/13 |
Antworten mit Zitat |
|---|---|---|
|
Bleibt die Frage, ob das wirklich so langsam ist, wie von dir angedeutet.
Vor allem, wenn man nur die Linien anderer Körper überprüft, wenn eine Kollision überhaupt möglich ist, sollten da doch pro Vertex nur ein paar Abfragen nötig sein. Nunja, aber ich will mich hier gar nicht zu sehr einmischen. Ihr habt von solchem Kram vermutlich mehr Ahnung als ich. |
||
|
Panic Pong - ultimate action mashup of Pong and Breakout <= aktives Spiele-Projekt, Downloads mit vielen bunten Farben!
advASCIIdraw - the advanced ASCII art program <= aktives nicht-Spiele-Projekt, must-have für ASCII/roguelike/dungeon-crawler fans! Alter BB-Kram: ThroughTheAsteroidBelt - mit Quelltext! | RGB-Palette in 32²-Textur / Farbige Beleuchtung mit Dot3 | Stereoskopie in Blitz3D | Teleport-Animation Screensaver |
||
|
|
ToeB |
Antworten mit Zitat |
|---|---|---|
|
Und noch ne Frage :
Kann man auch den winkel eines (z.b) Quadrates herausfinden, damit ich z.b eine Kiste darübermalen kann (die dann physikalisch berechnet wird) ? mfg ToeB |
||
|
Religiöse Kriege sind Streitigkeiten erwachsener Männer darum, wer den besten imaginären Freund hat.
Race-Project - Das Rennspiel der etwas anderen Art SimpleUDP3.0 - Neuste Version der Netzwerk-Bibliothek Vielen Dank an dieser Stelle nochmal an Pummelie, welcher mir einen Teil seines VServers für das Betreiben meines Masterservers zur verfügung stellt! |
||
|
|
hecticSieger des IS Talentwettbewerb 2006 |
Antworten mit Zitat |
|---|---|---|
|
Eine Verletintagration ist eine Konstruktion aus einfachen physikalischen Gegebenheiten. Es gibt demnach keine Quadrate, Würfel, Dreiecke oder Halbmonde, sondern nur die Positionen der Eckpunkte und dessen Verbindungen. Die Formen werden also nur von unserer Wahrnehmung festgestellt, das Programm ''weiß'' also nicht wie eine ''Form letztendlich aussieht''.
Bei meinem Physix habe ich zwei arten einer bildintegration eingesetzt: 1. Ein Bild wird an eine Eckpunktposition positioniert und dessen Winkelstellung angepasst. 2. Ein Bild wird an eine Verbindung geheftet und dessen Winkel ausgemessen und das Bild daran ausgerichtet. Der Winkel ergibt sich aus den Positionen der beiden zu verbindenen Eckpunkte +einem selbst anzugebenem und Winkelabhängigem Offset. Das Offset beinhaltet X und Y -Verschiebung und Rotationsoffset. Um den Winkel zweier Eckpunkte zu wissen, benötigst du deren Positionen die dann mit Atan2  verrechnet werden. verrechnet werden.
|
||
| Download der Draw3D2 V.1.1 für schnelle Echtzeiteffekte über Blitz3D | ||
|
|
ToeB |
Antworten mit Zitat |
|---|---|---|
|
Also "könnte" ich das so machen, das wenn ich diese 4 Punkte da habe, das ich dann den linkerenOberenPunkt mit der LinkerenOberenEcke verbinde etc. =?
(Wenn das iwie machbar ist in 2d) mfg ToeB |
||
|
Religiöse Kriege sind Streitigkeiten erwachsener Männer darum, wer den besten imaginären Freund hat.
Race-Project - Das Rennspiel der etwas anderen Art SimpleUDP3.0 - Neuste Version der Netzwerk-Bibliothek Vielen Dank an dieser Stelle nochmal an Pummelie, welcher mir einen Teil seines VServers für das Betreiben meines Masterservers zur verfügung stellt! |
||
|
|
hecticSieger des IS Talentwettbewerb 2006 |
Antworten mit Zitat |
|---|---|---|
|
Wenn du ein Kasten hast, dann wäre es ratsam einer Verbindung ein Bild anzuhängen. Da eine Verbindung dem Kasten abhängige Position und Rotation hat. Eine Verbindung liegt zwischen zwei Punkten. Ein Bild ausgehend eines Punktes in Richtung einer Verbindung geht irgendwie schlecht.
Du mußt es ja nicht benutzen, aber wenn du Blitz3D hast, kannst du dir die Draw3D mal anschauen. Da habe ich ein paar Beispiele die Bilder sowohl an Punkten als auch an Verbindungen angehängt sind. Andere einfache Möglichkeiten fallen mir nicht ein, wie man sonst Bilder an eine Verletintegration anhängen könnte. |
||
| Download der Draw3D2 V.1.1 für schnelle Echtzeiteffekte über Blitz3D | ||
|
|
tedy |
Antworten mit Zitat |
|---|---|---|
|
Kommt hier noch ein 2ter Teil ?
Ich fand den ersten Teil echt gut ! |
||
| 01010100 01100101 01000100 01111001 00100000 00111010 01000100 | ||
da_poller |
Antworten mit Zitat |
|
|---|---|---|
| jop und ich selbst hänge an in teil 2 kommender kollision | ||
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
Teil 2 kommt bestimmt... irgendwann. *hust*
Ich bin im Moment leider schon anderweitig ausgelastet, aber ich werde mich in dieser Woche mal dransetzen. Der zweite Teil wird leider extrem Mathematiklastig und daher ist es schwierig, ein angemessenes Tutorial zu schreiben - ich geb mir aber Mühe, es verständlich zu formulieren |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
da_poller |
Antworten mit Zitat |
|
|---|---|---|
|
joah mathe -.- daran haperts bei mir leider hab ja "nur qualli und da war nix mit geradengleichungen usw..
leider gottes.. und ne funktionierende funktion für hab ich noch nie zu stande gebracht |
||
|
|
Silver_Knee |
Antworten mit Zitat |
|---|---|---|
|
Also die Bisherige Mathemathiklastigkeit die ich erfahren musste war das kopieren von TimBos Code "Lines_Intersect" hier aus dem Codearchiv |
||
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
So, nach knapp 2 Monaten (schon so lange her?) gibt es nun endlich den Teil 2 von meinem Tutorial.
In diesem Teil werden wir die Grundlagen für die Kollision erarbeiten und einen Algorithmus schreiben, der zuverlässig Kollisionen erkennt. Vorausgesetzt wird eine Grundvorstellung darüber, was Vektoren sind - tieferes Wissen ist für das Verständnis von Vorteil. Dieser Teil ist noch nicht der letzte - die reine Kollisionserkennung bringt uns noch herzlich wenig Stoff des nächsten Tutorials wird dann sein, wie wir diesen Algorithmus mit unserer Verlet - Integration verbinden können, um eine ansehnliche Physik zu erhalten. Genug der langen Vorrede. Die Kollisionsmethode, die ich verwendet habe, nennt sich das "Separating Axis Theorem", welche sich in der Praxis sehr bewährt hat, weswegen wir diese verwenden werden. Wie funktioniert dieser Algorithmus? Wie der Titel schon andeutet, besagt die Theorie, dass zwei Objekte nicht kollidieren, solange man eine Gerade zwischen die beiden legen kann. 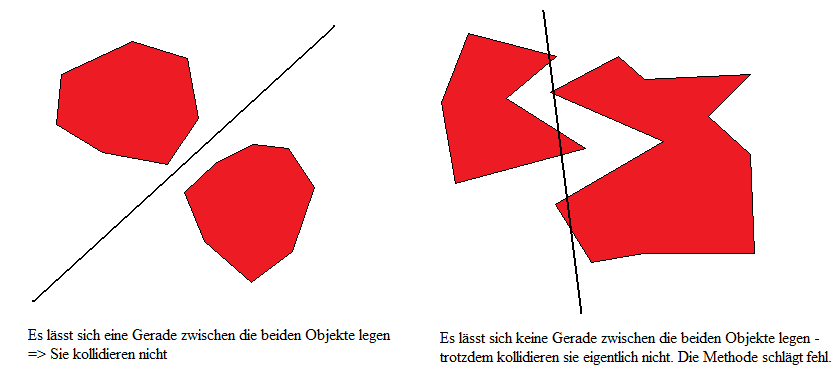
Der linke Teil des Bildes veranschaulicht, wie das gedacht ist. Das funktioniert schön und gut für alle 'konvexen' Objekte - salopp gesagt alle Objekte, die keine Löcher oder Gruben etc. besitzen. Versuchen wir, die Methode auf nicht-konvexe (=konkave) Objekte anzuwenden, so vermeldet der Algorithmus eine Kollision, obwohl eigentlich gar keine stattfindet - die rechte Seite zeigt eine solche Problemsituation. Diese Einschränkung muss uns im Moment noch nicht interessieren - wie wir solche Objekte trotzdem kollidieren lassen können, wird Bestandteil späterer Tutorials werden. Wir wissen nun also, was die Grundidee hinter dem SAT ist. Wie finden wir nun aber heraus, ob man eine Achse zwischen die beiden Objekte legen kann? Dies erreichen wir durch Projektion - wir projizieren nun nämlich die beiden Objekte auf eine Gerade und schauen, ob sich die Projektionen überlappen. Finden wir eine Gerade, auf der sich die Projektionen nicht überlappen, kollidieren die beiden Objekte nicht. 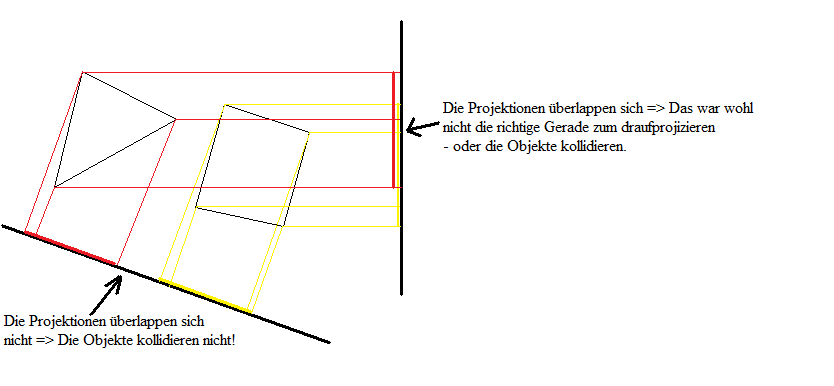
Das Bild zeigt, wie man sich das vorzustellen hat. Man geht einfach alle möglichen Geraden durch, projiziert beide Objekte drauf, und schaut, ob sich die Projektionen überlappen (eine Projektion einer 2D - Figur ist nichts weiteres als eine Linie). Findet man eine Gerade, auf der sich die Projektionen nicht überlappen, dann kollidieren die beiden Objekte nicht. Nur ist das nicht besonders effektiv - man kann nicht einfach mal so alle denkbaren Geraden ausprobieren, bis man eine findet, wo keine Überlappung stattfindet (falls die beiden Objekte nicht kollidieren). Es zeigt sich aber in der Praxis, dass es genügt, wenn man alle Verbindungen beider Objekte abklappert und auf eine Senkrechte auf die Verbindung projiziert. 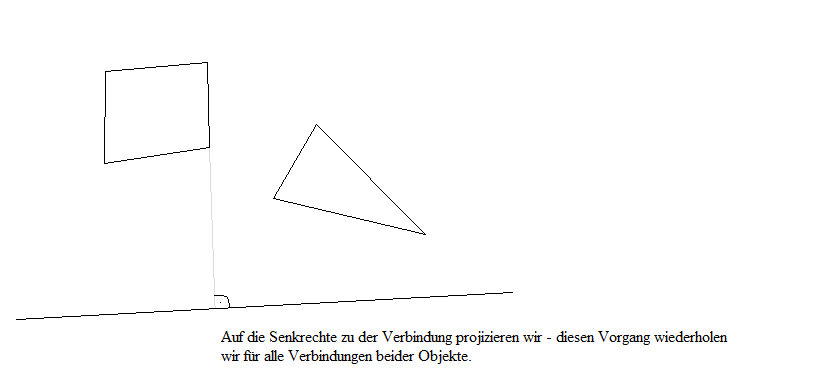
Das wäre es von der Theorie her - Zeit, das ganze in Code umzusetzen! Als erstes brauchen wir einen Entity - Type, der ein Physikobjekt darstellt. Dieser Type muss zum einen alle Partikel als auch alle Verbindungen aufnehmen können. Code: [AUSKLAPPEN] Type TEntity
Field VertexCount Field Vertex.TParticle[ MAX_VERTICES - 1 ] Field EdgeCount Field Edge.TConstraint[ MAX_EDGES - 1 ] End Type Die Types aus dem ersten Tutorial übernehmen wir. Als nächstes brauchen wir eine Funktion, die alle Objekte durchrattert und auf Kollisionen prüft: Code: [AUSKLAPPEN] Function UpdateCollisions()
For E1.TEntity = Each TEntity For E2.TEntity = Each TEntity If E1 <> E2 Then ProcessCollision( E1, E2 ) Next Next End Function Fehlt uns nur noch die Funktion ProcessCollision. Da das Berechnen der Reaktion auf die Kollision auch noch ein komplizierter Teil für sich sein wird, soll diese Funktion vorerst nichts tun, ausser die Kollisionen festzustellen und sie anzuzeigen. Die Kollisionsfunktion braucht noch ein paar Hilfsfunktionen, damit sie korrekt funktioniert. Als erstes benötigen wir eine simple Skalarprodukts - Funktion: Code: [AUSKLAPPEN] Function Dotproduct#( X1#, Y1#, X2#, Y2# )
Return X1#*X2# + Y1#*Y2# End Function Das Skalarprodukt kommt aus der Vektorgeometrie - da das hier kein Vektor - Tutorial ist, lasse ich das hier einfach mal stehen Als nächstes kommt eine Funktion, die uns ein Objekt auf eine Achse projiziert: Code: [AUSKLAPPEN] Function ProjectToAxis( AxisX#, AxisY#, Entity.TEntity )
Local DotP# = Dotproduct( AxisX#, AxisY#, Entity\Vertex[ 0 ]\X#, Entity\Vertex[ 0 ]\Y# ) ProjectedMin# = DotP# ProjectedMax# = DotP# For i = 1 To Entity\VertexCount - 1 DotP# = Dotproduct( AxisX#, AxisY#, Entity\Vertex[ i ]\X#, Entity\Vertex[ i ]\Y# ) If DotP# < ProjectedMin# Then ProjectedMin# = DotP# ElseIf DotP# > ProjectedMax# Then ProjectedMax# = DotP# Next End Function Übergeben wird eine Achse in Form von einem Vektor, AxisX# und AxisY#, und ein Physikobjekt, Entity.TEntity Als erstes wird der erste Punkt des Objekts auf die Achse projiziert - das geschieht mithilfe des Skalarprodukts. Von der Skalarprodukts - Funktion erhalten wir dann einen Zahlenwert zurück; er sagt uns gewissermassen, wo auf der Achse unser Punkt hinprojiziert wurde. Mitt dem Skalarprodukt projizieren wir nun die anderen Punkte einzeln auf die Achse und speichern jeweils den tiefsten und den höchsten Wert - dadurch erhalten wir die Aussenpunkte der Projektion. 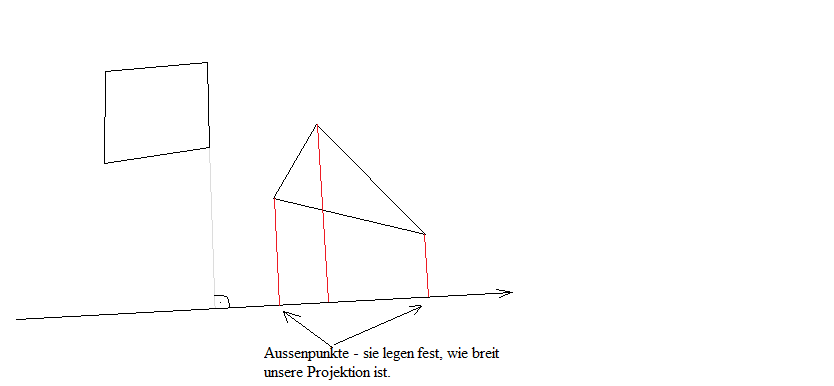
Da die Funktion eigentlich zwei Werte zurückliefern müsste (das linke und das rechte Ende der Projektion), müssen ProjectedMin# und ProjectedMax# global sein - da drin speichert die Funktion die errechneten Werte, die dann von ProcessCollision verwendet werden. Die nächste Funktion normalisiert uns einen Vektor, sprich, berechnet X# und Y# neu, dass die Länge des Vektors 1 ergibt. Da die Funktion auch zwei Parameter zurückgibt, müssen ResultX# und ResultY# ebenfalls global sein: Code: [AUSKLAPPEN] Function Normalize( X#, Y# )
Length# = Sqr( X#*X# + Y#*Y# ) ResultX# = X#/Length# ResultY# = Y#/Length# End Function Eine letzte Funktion fehlt uns noch - und zwar eine, die uns angibt, wie weit zwei Projektionen voneinander entfernt sind (überlappen sie, ist die Distanz kleiner als null): Code: [AUSKLAPPEN] Function IntervalDistance#( A1#, B1#, A2#, B2# )
If A1# < A2# Then Return A2# - B1# Else Return A1# - B2# EndIf End Function Die Funktionsweise ist relativ simpel. Da die Projektion des Physikobjekts auf eine Linie ja auch nur ein Linienabschnitt ist, müssen wir nur Start- und Endpunkte beider Linienabschnitte vergleichen. Start- und Endpunkt des Linienabschnitts sind auch nur einzelne Werte aus dem Skalarprodukt - einfacher gehts ja nicht mehr Das wären die Hilfsfunktionen - fehlt nur noch unsere Hauptfunktion! Code: [AUSKLAPPEN] Function ProcessCollision( E1.TEntity, E2.TEntity )
For i = 0 To E1\EdgeCount + E2\EdgeCount - 1 If i < E1\EdgeCount Then Edge.TConstraint = E1\Edge[ i ] Else Edge.TConstraint = E2\Edge[ i - E1\EdgeCount ] EndIf AxisX# = -( Edge\P2\Y# - Edge\P1\Y# ) AxisY# = Edge\P2\X# - Edge\P1\X# Normalize( AxisX#, AxisY# ) AxisX# = ResultX# AxisY# = ResultY# ProjectToAxis( AxisX#, AxisY#, E1 ) Min# = ProjectedMin# Max# = ProjectedMax# ProjectToAxis( AxisX#, AxisY#, E2 ) Distance# = IntervalDistance( Min#, Max#, ProjectedMin#, ProjectedMax# ) If Distance# > 0 Then Return False Next Return True End Function Um das Verständnis ein wenig zu erleichtern, erkläre ich jetzt Stück für Stück die Funktion. Code: [AUSKLAPPEN] For i = 0 To E1\EdgeCount + E2\EdgeCount - 1
If i < E1\EdgeCount Then Edge.TConstraint = E1\Edge[ i ] Else Edge.TConstraint = E2\Edge[ i - E1\EdgeCount ] EndIf Dieses seltsame Konstrukt sorgt dafür, dass ich nicht zwei Schleifen für beide Objekte brauche, sondern einen Codeabschnitt für beide Objekte verwenden kann. Die aktuell zu bearbeitende Seite wird einfach in Edge.TConstraint gespeichert und so verarbeitet. Code: [AUSKLAPPEN] AxisX# = -( Edge\P2\Y# - Edge\P1\Y# )
AxisY# = Edge\P2\X# - Edge\P1\X# Normalize( AxisX#, AxisY# ) AxisX# = ResultX# AxisY# = ResultY# Hier berechne ich die Senkrechte auf die aktuelle Seite und normalisiere den entsprechenden Vektor. Denkbar simpel. Code: [AUSKLAPPEN] ProjectToAxis( AxisX#, AxisY#, E1 )
Min# = ProjectedMin# Max# = ProjectedMax# ProjectToAxis( AxisX#, AxisY#, E2 ) Hier projiziere ich beide Objekte auf die vorhin errechnete Seite und habe dann den Achsenabschnitt in den Variablen Min#, Max#, ProjectedMin# und ProjectedMax#. Code: [AUSKLAPPEN] Distance# = IntervalDistance( Min#, Max#, ProjectedMin#, ProjectedMax# )
If Distance# > 0 Then Return False Hier berechne ich den Abstand der beiden Projektionen zueinander. Ist der Abstand grösser als null, überlappen die beiden Projektionen nicht, folglich kollidieren die Objekte nicht und es wird False zurückgeliefert. Wurde die Funktion vorher nicht durch ein 'Return False' verlassen, heisst das, es gibt keine Seite, auf der die Projektionen nicht überlappen => Die beiden Objekte kollidieren, also wird True zurückgegeben. Wie immer gibts nun ein kleines Beispiel, wo man die Kollisionserkennung ausprobieren kann. Einfach mit der Maus die Box bewegen, der Rest sollte selbsterklärend sein. Code: [AUSKLAPPEN] Const GWIDTH = 800
Const GHEIGHT = 600 Graphics GWIDTH, GHEIGHT, 0, 2 SetBuffer BackBuffer() Const MAX_VERTICES = 256 Const MAX_EDGES = 256 Const STEPSIZE = 12 Global ProjectedMin#, ProjectedMax# Global ResultX#, ResultY# Type TParticle Field X# Field Y# Field OldX# Field OldY# Field A_X# Field A_Y# Field Parent.TEntity End Type Type TConstraint Field P1.TParticle Field P2.TParticle Field Length# Field Parent.TEntity End Type Type TEntity Field VertexCount Field Vertex.TParticle[ MAX_VERTICES - 1 ] Field EdgeCount Field Edge.TConstraint[ MAX_EDGES - 1 ] Field Collision End Type Timer = CreateTimer( 60 ) SeedRnd MilliSecs() Mouse.TEntity = CreateBox( 200, 200, 50, 50 ) For i = 0 To 10 CreateBox( Rand( 0, GWIDTH ), Rand( 0, GHEIGHT ), Rand( 10, 50 ), Rand( 10, 50 ) ) CreateCircle( Rand( 0, GWIDTH ), Rand( 0, GHEIGHT ), Rand( 10, 50 ), Rand( 10, 50 ) ) Next While Not KeyHit( 1 ) Cls DiffX = MouseX() - Mouse\Vertex[ 0 ]\X DiffY = MouseY() - Mouse\Vertex[ 0 ]\Y For i = Mouse\VertexCount - 1 To 0 Step -1 Mouse\Vertex[ i ]\X = Mouse\Vertex[ i ]\X + DiffX Mouse\Vertex[ i ]\Y = Mouse\Vertex[ i ]\Y + DiffY Next UpdateCollision() Render() Flip 0 WaitTimer Timer Wend End Function UpdateCollision() For Entity.TEntity = Each TEntity Entity\Collision = 0 Next For E1.TEntity = Each TEntity For E2.TEntity = Each TEntity If E1 <> E2 Then E1\Collision = E1\Collision + ProcessCollision( E1, E2 ) Next Next End Function Function Render() LockBuffer BackBuffer() For Constraint.TConstraint = Each TConstraint If Constraint\Parent\Collision Then Color 255, 0, 0 Else Color 0, 255, 0 Line Constraint\P1\X#, Constraint\P1\Y#, Constraint\P2\X#, Constraint\P2\Y# Next For Particle.TParticle = Each TParticle If Particle\X# >= 0 And Particle\X# < GWIDTH Then If Particle\Y# >= 0 And Particle\Y# < GHEIGHT Then WritePixelFast Floor( Particle\X# ), Floor( Particle\Y# ), $00FFFFFF EndIf EndIf Next UnlockBuffer BackBuffer() End Function Function Min#( A#, B# ) If A# < B# Then Return A# Else Return B# End Function Function Max#( A#, B# ) If A# > B# Then Return A# Else Return B# End Function Function CreateParticle.TParticle( Parent.TEntity, X#, Y#, Mass# = 1 ) If Parent <> Null Then If Parent\VertexCount < MAX_VERTICES - 1 Then Particle.TParticle = New TParticle Particle\X# = X# Particle\Y# = Y# Particle\OldX# = X# Particle\OldY# = Y# Particle\Parent = Parent Parent\Vertex[ Parent\VertexCount ] = Particle Parent\VertexCount = Parent\VertexCount + 1 Return Particle EndIf EndIf End Function Function CreateConstraint.TConstraint( Parent.TEntity, P1.TParticle, P2.TParticle ) If Parent <> Null Then If Parent\EdgeCount < MAX_EDGES - 1 Then If P1 <> P2 Then Constraint.TConstraint = New TConstraint Constraint\P1 = P1 Constraint\P2 = P2 ConstraintLengthSq# = ( Constraint\P1\X# - Constraint\P2\X# )*( Constraint\P1\X# - Constraint\P2\X# ) + ( Constraint\P1\Y# - Constraint\P2\Y# )*( Constraint\P1\Y# - Constraint\P2\Y# ) Constraint\Length# = Sqr( ConstraintLengthSq# ) Constraint\Parent = Parent Parent\Edge[ Parent\EdgeCount ] = Constraint Parent\EdgeCount = Parent\EdgeCount + 1 Return Constraint EndIf EndIf EndIf End Function Function CreateBox.TEntity( X#, Y#, Width#, Height# ) Entity.TEntity = New TEntity P1.TParticle = CreateParticle( Entity, X# - Width#/2, Y# - Height#/2 ) P2.TParticle = CreateParticle( Entity, X# + Width#/2, Y# - Height#/2 ) P3.TParticle = CreateParticle( Entity, X# + Width#/2, Y# + Height#/2 ) P4.TParticle = CreateParticle( Entity, X# - Width#/2, Y# + Height#/2 ) CreateConstraint( Entity, P1, P2 ) CreateConstraint( Entity, P2, P3 ) CreateConstraint( Entity, P3, P4 ) CreateConstraint( Entity, P4, P1 ) CreateConstraint( Entity, P1, P3 ) CreateConstraint( Entity, P2, P4 ) Return Entity End Function Function CreateCircle.TEntity( X#, Y#, RadiusX#, RadiusY# ) Entity.TEntity = New TEntity For i = STEPSIZE To 360 Step STEPSIZE P.TParticle = CreateParticle( Entity, X# + Cos( i )*RadiusX#, Y# + Sin( i )*RadiusY# ) If i <> STEPSIZE Then CreateConstraint( Entity, P, Before P ) Next CreateConstraint( Entity, P, Entity\Vertex[ 0 ] ) Center.TParticle = CreateParticle( Entity, X#, Y# ) For i = 0 To Entity\VertexCount - 2 CreateConstraint( Entity, Entity\Vertex[ i ], Center ) Next Return Entity End Function Function Dotproduct#( X1#, Y1#, X2#, Y2# ) Return X1#*X2# + Y1#*Y2# End Function Function Normalize( X#, Y# ) Length# = Sqr( X#*X# + Y#*Y# ) ResultX# = X#/Length# ResultY# = Y#/Length# End Function Function ProjectToAxis( AxisX#, AxisY#, Entity.TEntity ) Local DotP# = Dotproduct( AxisX#, AxisY#, Entity\Vertex[ 0 ]\X#, Entity\Vertex[ 0 ]\Y# ) ProjectedMin# = DotP# ProjectedMax# = DotP# For i = 1 To Entity\VertexCount - 1 DotP# = Dotproduct( AxisX#, AxisY#, Entity\Vertex[ i ]\X#, Entity\Vertex[ i ]\Y# ) If DotP# < ProjectedMin# Then ProjectedMin# = DotP# ElseIf DotP# > ProjectedMax# Then ProjectedMax# = DotP# Next End Function Function IntervalDistance#( A1#, B1#, A2#, B2# ) If A1# < A2# Then Return A2# - B1# Else Return A1# - B2# EndIf End Function Function ProcessCollision( E1.TEntity, E2.TEntity ) For i = 0 To E1\EdgeCount + E2\EdgeCount - 1 If i < E1\EdgeCount Then Edge.TConstraint = E1\Edge[ i ] Else Edge.TConstraint = E2\Edge[ i - E1\EdgeCount ] EndIf AxisX# = -( Edge\P2\Y# - Edge\P1\Y# ) AxisY# = Edge\P2\X# - Edge\P1\X# Normalize( AxisX#, AxisY# ) AxisX# = ResultX# AxisY# = ResultY# ProjectToAxis( AxisX#, AxisY#, E1 ) Min# = ProjectedMin# Max# = ProjectedMax# ProjectToAxis( AxisX#, AxisY#, E2 ) Distance# = IntervalDistance( Min#, Max#, ProjectedMin#, ProjectedMax# ) If Distance# > 0 Then Return False Next Return True End Function Das wars - schon haben wir eine absolut zuverlässige Funktion, die uns alle Kollision korrekt und schnell berechnet. Leider reicht das noch nicht für unsere Verlet - Integration; wir müssen aus den Kollisionsdaten noch den Kollisionsvektor errechnen und den mithilfe kranker Matrizenrechnungen für eine Kollisionsantwort verwenden - bisher haben wir nur die Kollisionserkennung. Das ist dann aber Stoff für Teil 3 des Tutorials. Ich hoffe, ich konnte mich relativ verständlich ausdrücken und dass die Zeit bis zum dritten Teil nicht so lange wird wie bis zu diesem Teil (obwohl mir der Text leichter von der Hand ging als gedacht, mit guter Musik (=Mahou Shoujo Lyrical Nanoha A's Soundtrack) geht das doch recht einfach Na dann noch viel Spass mit dem Zusammenzimmern eurer eigenen Kollision. |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
Übersicht
 BlitzBasic
BlitzBasic  FAQ und Tutorials
FAQ und Tutorials
Powered by phpBB © 2001 - 2006, phpBB Group
