Kollisionen (minib3d, 3d raum)
Übersicht BlitzMax, BlitzMax NG
BlitzMax, BlitzMax NG  Beginners-Corner
Beginners-Corner
PhillipKBetreff: Kollisionen (minib3d, 3d raum) |
Antworten mit Zitat |
|
|---|---|---|
|
Huhu!
Nach stunden (mittlerweile Tagelangem <.<) umwälzen meiner Hirnwindungen und durchforsten unzähliger foreneinträge stehe ich immernoch da wo ich bereits vor 5 tagen stand: Kollisionen. Anfangs hab ich mir erst erarbeiten müssen, was 'Normals' sind, das verstehe ich nun endlich :> Aber egal wie sehr ich mich bemühe, ich kriege keine gescheihte Kollisionslogik geschrieben. Im moment habe ich ein Kollisionssystem, was entsprechende Speed-werte (SpeedY#, SpeedX, SpeedZ#) negiert, sobald der entsprechend größere normalwert (nach abs) ermittelt wurde. Das fuktioniert - zu meiner überraschung - ganz gut. Problem sind kanten, die bei CollisionNX() UND CollisionNZ() einen wert <>0 <>1 <>-1 liefern. Darum wollte ich meine logik umwälzen und eventuell eine winkelberechnung für den Austrittswinkel errechnen. Das problem ist, ich fürchte mir fehlt das grundlagen wissen aus der schule (Vektoren?) und entsprechendes Verständnis, wo genau ein Normalwert hinzeigt. In Blender konnte ich allderdings erfolgreich das prinzip der normalwerte nachvollziehen.. Aber ich verfang mich jedesmal, wenn ich versuche, simple logiken anhand von Normals zu errechnen(!) Solangsam bin ich echt deprimiert Des weiteren habe ich hier im Forum einmalig eine Winkelberechnung in einem 2d spiel gefunden, welches anhand von .. Vektoren?.. einen austrittwinkel berechnet. Diesen finde ich nun leider nichtmehr =/ Dachte mir eigentlich, das ich das auf meinen 3d Raum übertragen könnte.. Ich brauch eure hilfe Hier die formel: NeueRichtung = AlteRichtung - 2 * ((AlteRichtung * Normale) * Normale) (gefunden in irgendeinen Forum, wo es darum ging, eine Schläger-Ball kollision richtig darzustellen.. wohl irgendwie ein Baseball... auf jedenfall auf den 3d Raum bezogen) Ps: Ich arbeite momentan mit einem Eigenen TranslateEntity() was im prinzip so wirkt wie das normale.. Dazu habe ich pro objekt was sich bewegt eine SpeedX,SpeedY,SpeedZ variable und Translate diese jedesmal.. Ist das ein falscher ansatz? Gruß, ein verzweifelter Phillipk |
||
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
Diese "erstaunlich gut funktionierende" Formel ist genau das, was du suchst Die Sache mit Einfallswinkel = Aussfallswinkel lässt sich eigentlich nur in 2D gut umsetzen (und auch da ist es schon ein Gemurkse). In 3D wird es mit dieser Methode viel aufwändiger. Die Formel, die du hast, spiegelt einen Vektor an einem anderen Vektor. Den Vektor, den du spiegeln willst, ist deine Geschwindigkeit und den Vektor, an dem du spiegelst, ist die Oberflächennormale. Warum die Formel funktioniert, kann ich dir nicht sagen - da müsstest du irgendwo die Herleitung suchen, falls sie dich interessiert. PhilipK hat Folgendes geschrieben: Könnte mir jemand versuchen, das zu erklären? Dort werden die Normals benutzt.. alle? für jede koordinate einzeln? Was ist AlteRichtung?
Wie 'alle'? Es gibt doch nur eine? Und wie meinst du 'für jede Koordinate einzeln'? AlteRichtung in der Formel ist der Vektor mit deiner XYZ-Geschwindigkeit drin, in NeueRichtung steht dann der Vektor mit den Geschwindigkeiten nach dem Aufprall. |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
PhillipK |
Antworten mit Zitat |
|
|---|---|---|
|
Okay, womit wir beim problem der Vectoren sind.
Mir konnte bislang keiner genau erklären, was ein Vector ist. Bis lang habe ich nur so gearbeitet, dass ich mit Totalen X-Y-Z koordinaten unabhängig voneinander arbeite. Laut meinen recherchen ist ein 'Vector' eine position im Raum, per x-y-z angegeben. Aber .. mh? oO Mit "alle" meine ich, das meine jetzige einsetzung der formel so aussieht, das ich einfach mal als AlteRichtung meinen aktuellen X speed genommen hab & als normal den wert von CollisionNX() - dies für alle 3 koordinaten. Hier ergibt sich das problem, das der Vertikale speed (X und Z sind tiefe und breite, Y ist höhe) sich unterschiedlich auf x und z auswirkt. Und es scheint vorzukommen, das wenn mehrere Kollisionen stattfinden, der ball (okay, in meinem fall eine tomate Ich schaue noch einmal, ob ich irgendwo einen fehler finde (werte falsch eingesetzt? ich war ziemlich deprimiert als ich dauerhaft am googlen war^^)... Ansonsten: Wie wende ich die Formel auf XYZ (mein Vector :>) gleichermaßen an? In Minib3d habe ich eine TVector.bmx gefunden, welche alle rechenoperationen gleichermaßen auf XYZ anwendet, das ist - denke ich, hab keine ahnung Najut, ich merk schon, das thema braucht noch erlernbedarf (wenn ich mal was brauchbares finde^^)... Ich werde noch einmal alles überprüfen, und hoffen das mir meine Grauen Zellen noch ein wenig durch weitere hilfe aufgefrischt und angeregt werden =) Danke für die hilfe, Noo - ein kleiner hoffnugnsschimmer in meiner trauer =) Gruß, Phillipk ---- Edit: ich habe mir das nun mal genauer angeschaut.. Es scheint wirklich, als passen sich die kugeln dem untergrund an. Sah nur etwas verkorkst aus, weil dieser nicht wirklich "Soft" ist, sondern ein wenig kantig, da wir eine Lowpoly map bauen.. Der grund, warum mir das so ins auge gestochen ist, das ich gleichzeitig mein Springende-Bälle rausgehauen hab. War zu deprimiert das nachzuarbeiten und auf die neue Formel umzustellen.. Vorher war alles per if gelöst Ich werde mal gucken, ob dies nun Realistisch aussieht. Trotzdem würde ich mich über einen kleinen Exkurs zum Thema vectoren freuen. Tutorials oder Anfängerhilfen (links!) würden mir schon helfen ----- Edit2: Es scheint trotzdem nicht ganz so zu laufen Benötige also dringend erklärung ^^" 1) Gibt es irgendwelche bedingungen, wann das Spiegeln eines 'Vectors' an einem anderen 'Vector' nicht sinnvoll ist? Bzw anders gefragt: wie sieht das spiegeln aus? Wenn ich die werte per hand nachrechne, krieg ich nur stunk raus. Aber im Projekt siehts 'fast' perfekt aus.. 2) Zum fast perfekt: Es gibt ein paar stellen, da scheinen die Collisions zu buggen. Als würde sie auf einer fläche nebenan stattfinden. Es ist eine Sphere->Poly collision. Gibts da irgendwelche bekannten unstimmigkeiten? 3) In dem Forum wo ich die formel herhabe gab es auch den rat, die normals aus umliegenden flächen zusammenzurechnen, um einen besseren Richtungswert zu erhalten, da es sonst schon extrem viele Polys braucht, bis es einigermaßen passend aussieht. Wie könnte ich solche flächen erarbeiten? Und wichtiger, wie kriege ich den Punkt der Fläche raus, wo die collision stattgefunden hat? CollisionX() etc liefern mir anscheind zu ungenaue ergebnisse, als das ich diese als allgemeingütlig abstempeln kann. Gruß, Phillipk |
||
|
|
M0rgenstern |
Antworten mit Zitat |
|---|---|---|
|
@Noobody, warum wirds in 3D viel aufwendiger? Du kannst doch für Vektoren wie gleichen Formeln nutzen.
Der Sonderfall Ball berührt Wand und Boden gleichzeitig muss dann halt ein wenig blöd gehandhabt werden nämlich: Erst das eine dann das andere. Also man berechnet die Kollision mit der Wand undmit dem neuen Ergebnis die Kollision mit dem Boden. Man kann ja mit einer einfachen Formel den WInkel zwischen der Wand und dem Objekt berechnen. Dann muss man einen Vektor finden, der wieder von der Wand weggeht und den gleichen Winkel zur Wand hat wie das Objekt beim Eintreffen. Hier muss auch gelten: Winkel zwischen beiden Vektoren = 180 - (Eintrittswinkel + Austrittswinkel) => 180 - (2*Einfallswinkel). Also muss man die Formel nur so umstellen, dass man einen Vektor erhält der oben genannten Winkel zum EintrittsVektor hat. Das müsste eigentlich mit einer einzigen Formel gehen. Lg, M0rgenstern |
||
|
|
mpmxyz |
Antworten mit Zitat |
|---|---|---|
|
Hallo PhillipK,
ein Vektor ist einfach ein Wert mit einer Größe und einer Richtung. In der Regel werden diese durch Komponenten - z.B. x, y und z - dargestellt. Diesen Wert kann man nun als eine Geschwindigkeit, eine Position oder einen Weg interpretieren. Das Addieren zweier Vektoren entspricht dem Aneinanderhängen dieser. Dabei werden jeweils die einzelnen Komponenten der beiden Vektoren addiert. Ein Vektor kann gestreckt, gestaucht und gespiegelt werden, indem man ihn mit einer Zahl multipliziert. Dabei wird einfach jede komponente mit dieser Zahl multipliziert. Man kann auch zwei Vektoren miteinander multiplizieren. Hierbei gibt es zwei Möglichkeiten. Das, was in der Formel steht, ist das Skalarprodukt. Es hängt von der Länge der Vektoren und dem Winkel, den diese miteinander bilden, ab. Man kann es einfach berechnen, indem die Komponenten des einen Vektors mit den Komponenten des anderes Vektors multipliziert werden und man daraus die Summe bildet. (Vektor1*Vektor2=x1*x2+y1*y2+z1*z2) Hierbei kommt eine Zahl heraus. Das andere Produkt, dass man mit Vektoren bilden kann, ist das Vektorprodukt. Hierbei kommt ein Vektor als Ergebnis heraus, welcher senkrecht zu den beiden multiplizierten Vektoren steht. (Die Formel lasse ich mal weg, weil dieses Produkt hier nicht gebraucht wird.) mfG mpmxyz PS: M0rgenstern, ich möchte sehen, wie du die Winkel im dreidimensionalen Raum berechnest. Edit: PhillipK, stelle einfach Fragen, wenn dir meine Kurzbeschreibung zu kurz ist! |
||
|
Moin Moin!
Projekte: DBPC CodeCruncher Mandelbrot-Renderer |
||
- Zuletzt bearbeitet von mpmxyz am Mi, Nov 03, 2010 21:23, insgesamt 4-mal bearbeitet
|
|
M0rgenstern |
Antworten mit Zitat |
|---|---|---|
|
@mpmxyz:
Den Winkel kann man ganz einfach so berechnen: cos(phi) = (VektorA * VektorB) / (|VektorA| * |VektorB|) Das was du ja eigentlich schon gesagt hast und das ganze ist auch im Dreidimensionalen Raum definiert. Was genau ist in der Formel die Phillip geschrieben hat mit normale gemeint? Der normierte Vektor? Blick da durch die Formel nicht so ganz durch und durch deine Erklärung, mpmxyz, leider auch nicht ganz. Mit dem Skalarprodukt kannst du ja den Winkel ausrechen, aber welcher Vektor soll denn jetzt rechtwinklig auf den beiden anderen stehen? Mit dem Vektorprodukt kommt man hier glaube ich so nicht weiter. Korrigier mich wenn ich falsch liege, ich komm nur grade nicht mit was genau du meinst. Lg, M0rgenstern |
||
|
|
mpmxyz |
Antworten mit Zitat |
|---|---|---|
|
Normalen scheint er durch Blender schon verstanden zu haben. (Stichwort: Ausrichtung der Oberflächen) Die Formel, mit der man die Winkel berechnen kann, ist mir bekannt. (dir wohl auch Wie kommt man aber damit weiter? Auch auf diese Frage gibt es eine Antwort, welche aber noch viel mehr Mathematik braucht. Da ist es besser, wenn man die andere Formel nutzt, anstatt auf Winkeln zu beharren. Zu meiner Wand an Text: Das soll ein kleiner Crashkurs zu Vektoren sein. Den einen leicht missverstehbaren Punkt mit dem Vektorprodukt habe ich deutlicher gemacht. mfG mpmxyz PS: Bei der letzten Aufforderung habe ich versucht, ein Totschlagargument loszulassen. Meine Einschätzung, dass du die Winkel empfohlen hast, weil du die Formel dazu nicht kennst, war aber leicht falsch. Der Versuch schlug fehl. Edit: Ich habe nun auch die umständliche Definition des Skalarprodukts weggenommen. |
||
|
Moin Moin!
Projekte: DBPC CodeCruncher Mandelbrot-Renderer |
||
- Zuletzt bearbeitet von mpmxyz am Mi, Nov 03, 2010 21:22, insgesamt einmal bearbeitet
|
|
M0rgenstern |
Antworten mit Zitat |
|---|---|---|
|
Was ich an deiner Erklärung nicht verstanden habe ist das hier:
Zitat: (Vektor1*Vektor2=Betrag von Vektor 1*Betrag von Vektor2*Cos(Winkel zwischen den Vektoren)=x1*x2+y1*y2+z1*z2 Betrag=Länge)
Versuchst du da das Skalarprodukt zu erklären? Das mit dem WInkel war ja nur ein Ansatz der vielleicht nicht so dolle ist, weil er etwas schwieriger umzusetzen ist. Aber wie willst du mit dem Vektorprodukt weiter kommen? Dann bekommst du nur einen Vektor raus, der Senkrecht auch den anderen beiden steht. Oder willst du den gar nicht benutzen, um das Problem zu lösen, sondern nur weil du das Vektorprodukt erklären willst? Wegen dem "Toschlagargument": Das hab ich direkt gemerkt. Aber hier verweise ich hierauf: BlitzMax: [AUSKLAPPEN] https://www.blitzforum.de/forum/viewtopic.php?t=35991
Ist zwar nicht dreidimensional, aber das tut ja nichts zur Sache. Ist aber schon okay Lg, M0rgenstern |
||
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
Zu der Sache mit den Winkeln: Man kann es so machen, durchaus. Allerdings wird es dann sehr kompliziert. Du hast zwar eine tolle Formel gepostet, mit der man den Winkel zwischen zwei Vektoren berechnen kann, aber von da an weiter?
Tatsächlich muss man nämlich den Vektor in sphärische Koordinaten umrechnen, zu Phi 180° addieren und wieder zu normalen Koordinaten zurückrechnen. Es funktioniert - aber ist viel komplizierter und langsamer. PhilipK hat Folgendes geschrieben: Mit "alle" meine ich, das meine jetzige einsetzung der formel so aussieht, das ich einfach mal als AlteRichtung meinen aktuellen X speed genommen hab & als normal den wert von CollisionNX() - dies für alle 3 koordinaten.
Ui, das ist natürlich falsch. Du hast folgende Formel: NeueRichtung = AlteRichtung - 2 * ((AlteRichtung * Normale) * Normale) Lösen wir die mal von innen nach aussen auf. Normale ist ein Vektor. AlteRichtung ist ein Vektor. AlteRichtung*Normale ist also das Skalarprodukt von AlteRichtung und Normale. Das funktioniert so, dass du das X von AlteRichtung mit dem X von Normale multiplizierst (dasselbe mit Y und Z) und du dann die einzelnen Produkte wieder addierst. Also: BlitzMax: [AUSKLAPPEN] Local Skalarprodukt:Float = AlteRichtungX*NormaleX + AlteRichtungY*NormaleY + AlteRichtungZ*NormaleZ Hier kommt also eine Zahl heraus. Normale ist immer noch ein Vektor. Das heisst, bei der zweiten Multiplikation in der Klammer müssen wir eine Zahl mit einem Vektor multiplizieren. Das funktioniert ganz einfach BlitzBasic: [AUSKLAPPEN] Local ProduktX:Float = Skalarprodukt*NormaleX Schon haben wir die Klammern aufgelöst! Vor der Klammer steht aber ein 2*. 2 ist eine Zahl, und in der Klammer ist am Ende wieder ein Vektor herausgekommen (Zahl mal Vektor gibt wieder einen Vektor). Das heisst, wir multiplizieren wieder eine Zahl mit einem Vektor BlitzMax: [AUSKLAPPEN] ProduktX = 2.0*ProduktX Wie wir sehen, bekommen wir wieder einen Vektor heraus. Am Ende haben wir hier noch AlteRichtung - xxxx stehen. AlteRichtung ist ein Vektor, 2*Klammer ist auch ein Vektor - sprich, wir subtrahieren hier einen Vektor von einem Vektor. Das ist auch relativ simpel BlitzMax: [AUSKLAPPEN] Local NeueRichtungX:Float = AlteRichtungX - ProduktX Am Ende kommt wieder ein Vektor heraus. Und was ist das genau für ein Vektor? Richtig, die neue Geschwindigkeit, nachdem sie an der Normalen gespiegelt wurde. Wie genau man sich das vorstellen kann, ist aus folgender Skizze zu entnehmen: 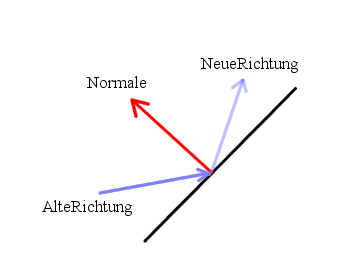
Wenn wir hier an den Anfang von AlteRichtung noch einen Ball hinzudenken, sehen wir, dass das stimmen muss - so ungefähr prallt nämlich ein Ball von einer Wand ab. Die Formel zu erklären wird natürlich ein wenig schwierig, wenn du nicht viel von Vektorgeometrie verstehst. Im Prinzip berechnen wir mit dem Skalarprodukt den Teil von AlteRichtung, der parallel zu der Normale liegt. Wenn wir die Normale mit diesem Betrag multiplizieren und von AlteRichtung subtrahieren, würde die neue Richtung genau senkrecht zur Normalen stehen. Subtrahieren wir sie aber doppelt (daher das *2), kommt die neue Richtung genau gespiegelt zur Normalen heraus. Wenn dich das interessiert, kann ich dir noch eine Skizze basteln, um das Prinzip dahinter zu erklären versuchen. Ich hoffe, das hilft dir weiter. |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
|
|
M0rgenstern |
Antworten mit Zitat |
|---|---|---|
|
Achso ist das gemeint.
Seh ich das richtig, dass die Normale der Vektor ist, der a) senkrecht auf der Ebene steht von der das Objekt abprallt und b) genau dort angesiedelt ist, wo das Objekt aufprallt? Eine Sache noch: Mit NeueRichtung bzw AlteRichtung ist doch die Geschwindigkeit gemeint, oder? Also, das wär für mich das einzig logische. Wie gesagt, das mit den Winkeln geht, aber das ist halt viel komplizierter, war ja nur sone Spontanidee. Lg, M0rgenstern |
||
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
M0rgenstern hat Folgendes geschrieben: Seh ich das richtig, dass die Normale der Vektor ist, der a) senkrecht auf der Ebene steht von der das Objekt abprallt und b) genau dort angesiedelt ist, wo das Objekt aufprallt?
Zu A: Eine Oberflächennormale steht senkrecht zu der Oberfläche, anhand derer sie erstellt wurde, ja. Zu b: Du scheinst da etwas falsch zu verstehen; Vektoren haben keine Position. Die Normale kannst du frei im Raum positionieren - sie stellt ja nur eine Richtung dar. (es gibt zwar Ortsvektoren, die man als Position interpretieren kann, aber im Prinzip sind auch die nur eine Richtung) |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
PhillipK |
Antworten mit Zitat |
|
|---|---|---|
|
Wuhu o_O
Nach 10 stunden schlaf bin ich erwacht & quähl mich gleich mit weiterlernen Nun, ich habe erstmal alles aufgenommen und werde mich jetzt ans nachdenken begeben. Ich denke, so ausführlich wie Noo das erklärt hat, kann garnichts schiefgehen Ich wette, ich werde hier noch ein - zwei nachfragen haben.. Dann melde ich mich wieder Aber eins weiß ich: Vektoren klingen intressant. Das ist definitv ein Thema, was ich mir mal erarbeiten sollte *g* Zumal mich Mathe immer schon ein wenig intressiert hat @M0rgenstern: Eine Normale Zeigt dir grob gesagt, die richtung in X-Y-Z offsets, wo die fläche hinzeigt. Sie ist allerdings nicht immer dort angesiedelt, wo das Objekt abprallt, sondern bildet nur den Richtungszeiger der Fläche.. Du kannst eigentlich davon ausgehen, das eine gleiche fläche auch nur in eine richtung Zeigt (Das ist so ein bisschen wissen, was ich mir schon erarbeitet habe.. Zerreißt mich, wenns totaler humbug ist, ich habs ohne Vektoren-Wissen versucht zu erklären ^^) Vielen dank für eure Hilfe Gruß, Phillip |
||
|
|
M0rgenstern |
Antworten mit Zitat |
|---|---|---|
|
@Noobody:
Verzeih, ich war gestern nicht ganz bei der Sache. Vektoren geben natürlich keine direkte Position an. Das mit der Normale habe ich heute dann auch irgendwo im Buch gesehen. Lg, M0rgenstern |
||
Übersicht
 BlitzMax, BlitzMax NG
BlitzMax, BlitzMax NG  Beginners-Corner
Beginners-Corner
Powered by phpBB © 2001 - 2006, phpBB Group
