Mathematisches Problem
Übersicht Sonstiges
Sonstiges  Smalltalk
Smalltalk|
|
hazumu-kunBetreff: Mathematisches Problem |
Antworten mit Zitat |
|---|---|---|
Für eine technische Zeichnung muss ich folgendes Problem lösen:
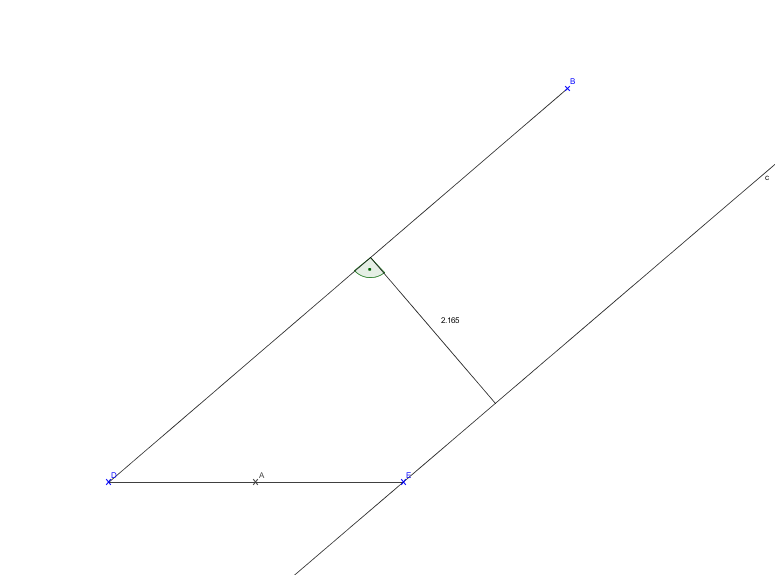
Gegeben: Die Punkte A(5|0) ,B(30|20) und der Abstand der Parallelen(2,165). A ist Mittelpunkt der Strecke DE. Gesucht: Länge der Strecke AD Ansatz: AD=AE=1/2 DE Und weiter komme ich nicht, ich hab mir schon ausgiebig Gedanken dazu gemacht, und auch Die Zeichnung ein wenig ausgebaut, aber ich komme nicht vorran. Hat jemand einen Geistesblitz? Danke schonmal im vorraus. p.s.: Das ist keine Mathehausaufgabe die ihr mir lösen sollt, es geht hier um rein privates Interesse. Wäre ja auch abstrus in der 12 nochmal mit klassischer Geometrie anzufangen. |
||
|
Warum kann es keine omnipotente Macht geben?
Weil diese omnipotente Macht in der Lage sein müsste, einen so schweren Stein zu schaffen, dass sie ihn nicht heben kann -> nicht omnipotent |
||
- Zuletzt bearbeitet von hazumu-kun am Do, Jan 13, 2011 18:27, insgesamt 3-mal bearbeitet
|
|
BladeRunnerModerator |
Antworten mit Zitat |
|---|---|---|
| Ohne Kenntnis der Winkel zu den Parallelen seh ich da wenig Chance, denn es gibt ja unendlich viele Möglichkeiten wie die Strecke DE zu den Parallelen liegen kann. | ||
|
Zu Diensten, Bürger.
Intel T2300, 2.5GB DDR 533, Mobility Radeon X1600 Win XP Home SP3 Intel T8400, 4GB DDR3, Nvidia GF9700M GTS Win 7/64 B3D BMax MaxGUI Stolzer Gewinner des BAC#48, #52 & #92 |
||
|
|
hazumu-kun |
Antworten mit Zitat |
|---|---|---|
|
Das hab ich mir schon fast gedacht, Problem ist, das der Winkel wiederrum erst durch den Abstand der Punkte A und D berechenbar wird.
EDIT: Ich vergaß noch ein paar Koordinaten anzugeben, vllt hilft das. (Koords im Startpost.) |
||
|
Warum kann es keine omnipotente Macht geben?
Weil diese omnipotente Macht in der Lage sein müsste, einen so schweren Stein zu schaffen, dass sie ihn nicht heben kann -> nicht omnipotent |
||
|
|
M0rgenstern |
Antworten mit Zitat |
|---|---|---|
|
Du könntest es folgendermaßen versuchen:
Man kann hier zwei rechtwinklige Dreiecke einzeichnen: Ein größere, wenn man das Lot von E auf die Gerade fällt. Die Höhe des Dreiecks auf den Punkt A Teilt das Dreieck dann nochmal in zwei rechtwinklige Dreiecke und teilt den rechten Winkel genau in der Hälfte. Wenn du dann das Lot von A auf die Gerade fällst, erhälst du mit der Höhe von dem anderen Dreieck nochmal ein rechtwinkliges Dreieck, von dem du folgende Dinge weißt: 1) Die Ankathete ist 2,165/2 2) Die Gegenkathete ist vielfaches von (Lotpunk-B) 3) Zwei Winkel: 90° und 45° Woraus du folgendes ableiten kannst: Der letzte Winkel ist auch 45° Somit kannst du auch die Gegenkathete ausrechnen. Dadurch kennst du auch den Lotfußpunkt von E und kannst damit auch E ausrechnen. Der Rest dürfte dann nicht mehr schwer sein. Also, ich gehe mal davon aus, dass die Lagebeziehung auch so ist wie sie anschaulich dargestellt ist, also DE waagerecht. Die Höhe des großen rechtwinkligen Dreiecks trifft nämlich genau auf A. Vllt kann dir das ja helfen. Vllt ein wenig mit Vektoren arbeiten, dürfte einfacher sein. Lg, M0rgenstern Edit: Die Ankathete sollte 2,165/2 sein. Ganz sicher kann du das aber berechnen indem du die länge des Vektors AA' ausrechnest, wobei A' halt der Lotpunkt ist. |
||
|
|
hazumu-kun |
Antworten mit Zitat |
|---|---|---|
|
Die Höhe des Dreiecks geht eben nicht auf den Punkt A, nicht zwingend.
Ich muss die Zeichnung wohl anders konzipieren. |
||
|
Warum kann es keine omnipotente Macht geben?
Weil diese omnipotente Macht in der Lage sein müsste, einen so schweren Stein zu schaffen, dass sie ihn nicht heben kann -> nicht omnipotent |
||
|
|
Tankbuster |
Antworten mit Zitat |
|---|---|---|
|
Wie liegt D-A-E denn?
müssen die Punkte D und E auf jeweils einer geraden liegen? Wo genau denn? Wenn sie überall liegen könnten, ist die Strecke ja auch immer unterschiedlich lang, da es dann unendlich Möglichkeiten für die Strecke D-A-E gibt. Also müssen die Koordinaten von D oder E gegeben sein oder immerhin begrenzt sein. |
||
|
Twitter
Download Jewel Snake! Windows|Android |
||
|
|
M0rgenstern |
Antworten mit Zitat |
|---|---|---|
|
Also, wenn man annimmt, was auf der Skizze zu sehen ist, also: D liegt auf einer der Geraden und E liegt auf einer der Geraden undzwar in gleicher Höhe, dann ist dem schon so.
Wenn aber D und E unterschiedlich hoch liegen, dann kann man davon natürlich nicht mehr ausgehen. Sollte ja nur ein Ansatz sein. Lg, M0rgenstern |
||
|
|
hazumu-kun |
Antworten mit Zitat |
|---|---|---|
|
Wie DAE genau liegt kann man nicht beschreiben, da B theorethisch als Drehpunkt dienen kann, das Problem bleibt das selbe.
@Morgenstern: Die Zeichnung sagt nichts genaues aus, weil um eine maßstäbliche Zeichnung zu erstellen, muss ich das Problem lösen, und um das Problem zu lösen brauche ich anscheinend eine maßstäbliche Zeichnung o.o. Ich habe mich jetzt entschlossen für die Konstruktion meiner Papierbrücke (Schülerwettbewerb der Uni Siegen) einen anderen Ansatz zu wählen. |
||
|
Warum kann es keine omnipotente Macht geben?
Weil diese omnipotente Macht in der Lage sein müsste, einen so schweren Stein zu schaffen, dass sie ihn nicht heben kann -> nicht omnipotent |
||
|
|
BigMaexle |
Antworten mit Zitat |
|---|---|---|
|
Quatsch, geht doch.
Wenn man davon ausgeht, dass DE waagerecht ist, ist doch alles da? Ein bisschen Trigonometrie, ein bisschen Pythagoras und schwuppeldidup: AE = 1,732845 |
||
|
--------------------------------------
Ich bin unfreiwillig ein Mitglied dieser kapitalistischen Gesellschaft, wo jeder Geldgeile Unternehmer an mein Geld will und ich selbst bei meinen Entscheidungen so gut wie willenlos bin...... und ich bin glücklich drüber |
||
|
|
blackgecko |
Antworten mit Zitat |
|---|---|---|
|
Zitat: Gegeben:
Die Punkte A(5|0) ,B(30|20) und der Abstand der Parallelen(2,165). A ist Mittelpunkt der Strecke DE. Wo liest du da, dass DE waagerecht ist? Die Strecke kann liegen wie sie will. |
||
|
So long and thanks for all the fish.
Fedora 17 | Windows 7 || BlitzPlus | BlitzMax Rechtschreibflame GO!!! Deppenapostroph | SeidSeit | Deppenakzent | DassDas | Deppenleerzeichen | TodTot | enzigste.info - Ja, ich sammel die. |
||
|
|
BigMaexle |
Antworten mit Zitat |
|---|---|---|
|
Aus der Zeichnung, tzzz |
||
|
--------------------------------------
Ich bin unfreiwillig ein Mitglied dieser kapitalistischen Gesellschaft, wo jeder Geldgeile Unternehmer an mein Geld will und ich selbst bei meinen Entscheidungen so gut wie willenlos bin...... und ich bin glücklich drüber |
||
|
|
ToeB |
Antworten mit Zitat |
|---|---|---|
|
Trotzdem hat das NIX mit phythagoras szu tun, tzzz mfg ToeB |
||
|
Religiöse Kriege sind Streitigkeiten erwachsener Männer darum, wer den besten imaginären Freund hat.
Race-Project - Das Rennspiel der etwas anderen Art SimpleUDP3.0 - Neuste Version der Netzwerk-Bibliothek Vielen Dank an dieser Stelle nochmal an Pummelie, welcher mir einen Teil seines VServers für das Betreiben meines Masterservers zur verfügung stellt! |
||
|
|
Arrangemonk |
Antworten mit Zitat |
|---|---|---|
|
a ist der mittelpunkt der strecke de, also liegt er auch in der mitte der parallelen
-> kreis um a mit radius (abstand der parralellen /2) die eine der tangenten durch b ist deine eine parallele, da machst du ne senkrechte drauf, die durch a geht, und am schnittpunkt zwischen der senkrechten und dem kreis, machst du ne andere gerade, die senkrecht zur ersten senkrechten ist damit hast du schonmal die beiden parallelen edit: wenn du jetzt noch nen winkel oder nen weiteren punkt hergeben kannst, dann kann man das auch zeichnen, weil so ist das ein unterbestimmtes gleichungsystem, und jede strecke durch a, die die beiden parallelen (also alle bis auf eine weitere parallele) wär eine lösung |
||
| ingeneur | ||
Übersicht
 Sonstiges
Sonstiges  Smalltalk
Smalltalk
Powered by phpBB © 2001 - 2006, phpBB Group
