gluProject [Gelöst]
Übersicht BlitzMax, BlitzMax NG
BlitzMax, BlitzMax NG  Allgemein
Allgemein|
|
VertexBetreff: gluProject [Gelöst] |
Antworten mit Zitat |
|---|---|---|
|
Hallo,
für ein kleines Augmented Reality Projekt, möchte ich gegebene 2D-Koordinaten eines mit einer Webcam aufgenommen Quadrats in eine Model-View-Matrix umsetzen. Über das Webcam-Bild soll dann ein 3D-Objekt gezeichnet werden, wobei das Quadrat als Boden dient. Dazu muss ich aber verstehen, wie bei OpenGL 3D-Koordinaten in 2D-Koordinaten projeziert werden. Dazu gibt es die Funktion gluProject. Sie nimmt die Objekt-Koordinaten (objX, objY, objZ), die Model-View-Matrix m, die Projection-Matrix p, und den Viewport (viewX, viewY, viewWidth, viewHeight) entgegen, und gibt die Screen-Koordinaten in (winX, winY, winZ) aus. Dazu folgendes Beispiel: Der Vektor v = (1,0,0,1) soll in Screen-Koordinaten projeziert werden. Der Viewport ist (0,0,640,480) und die Model-view-Matrix sowie die Projection-Matrix sind gegeben: BlitzMax: [AUSKLAPPEN] SuperStrict Die Screen-Koordinaten (395,241) stimmen genau überein, als würde ich mit diesen Bedingungen in OpenGL den Punkt über glVertex4f(1.0,0.0,0.0,1.0) zeichnen. Zum Problem Mein Problem ist, dass ich die Rechnung von gluProject nicht manuell nachvollziehen kann. In der Doku (und auch im Quellcode von Mesa) wird folgendes Berechnet: v'' = P x M x v winX = view(0) + (view(2)*(v''(0) + 1)) / 2 winY = view(1) + (view(3)*(v''(1) + 1)) / 2 winZ = (v''(2) + 1) / 2 Also v'' sind offensichtlich die homogenen Screen-Koordinaten, wenn man sich den Bildschirm als 2x2x2 großen Würfel vorstellt. winX und winY die Screen-Koordinaten, wenn man sich den Bildschirm als 640x480x2 großen Quader vorstellt. Jetzt versuche ich die Rechnung per Hand durchzuführen: v'' = P x M x v und heraus kommt: Also kommt hier v'' = (1.28716, 0.0280047, 5.29449, 5.489) heraus. Und nun von v'' zu (winX, winY, winZ): winX = 0 + (640*(1.28716 + 1)) / 2 = 731.8912 winY = 0 + (480*(0.0280047 + 1)) / 2 = 246.721128 winZ = (5.29449 + 1) / 2 = 3.147245 Erwartet (nach gluProject) hatte ich (winX, winY, winZ) = (395.03912899800036, 241.22447338029326, 0.98228176877347739) Händisch habe ich allerdings berechnet: (winX, winY, winZ) = (731.8912, 246.721128, 3.147245) Also vollkommen andere Screen-Koordinaten. Hat dafür jemand eine Erklärung? Schließlich sind die Matrizen, die ich Wolfram Alpha übergeben habe, die selben, die ich gluProject übergeben habe. Ciao Olli |
||
| vertex.dreamfall.at | GitHub | ||
- Zuletzt bearbeitet von Vertex am Fr, Okt 28, 2011 15:49, insgesamt einmal bearbeitet
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
Seltsamerweise steht das nicht in der Formel, aber du musst die homogenen Bildschirmkoordinaten durch w (die vierte Komponente von v'') teilen, bevor du sie zur Berechnung der Pixelkoordinaten verwenden darfst.
Wenn ich das so in MATLAB ausprobiere, gibt das dieselben Koordinaten wie gluProject Code: [AUSKLAPPEN] >> P = [1.81066, 0, 0, 0; 0, 2.4142, 0, 0; 0, 0, -1.002, -2.002; 0, 0, -1, 0]
P = 1.8107 0 0 0 0 2.4142 0 0 0 0 -1.0020 -2.0020 0 0 -1.0000 0 >> M = [0.9739, 0, 0.22665, -0.2634155; 0.1036, 0.8894, -0.4452, -0.09272; -0.20158, 0.45709, 0.86626, -5.28885; 0, 0, 0, 1] M = 0.9739 0 0.2266 -0.2634 0.1036 0.8894 -0.4452 -0.0927 -0.2016 0.4571 0.8663 -5.2889 0 0 0 1.0000 >> v = P*M*[1;0;0;1] v = 1.2864 0.0263 3.4994 5.4904 >> v = v./v(4) v = 0.2343 0.0048 0.6374 1.0000 >> [(640*(v(1) + 1))*0.5, (480*(v(2) + 1))*0.5, (v(3) + 1)*0.5] ans = 394.9782 241.1482 0.8187 |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
|
|
Vertex |
Antworten mit Zitat |
|---|---|---|
|
Vielen, vielen Dank! Es funktioniert, obwohl das dann nicht mehr mit Hilfe einer linearen Transformation beschrieben werden kann.
Habe v''_x = v''_x \ v''_w, ... im Mesa-Quelltext übersehen, in der Doku steht es blöderweise nicht. Also nochmal Danke! |
||
| vertex.dreamfall.at | GitHub | ||
|
|
Firstdeathmaker |
Antworten mit Zitat |
|---|---|---|
|
Hi,
ich arbeite zur Zeit auch an einem AR-Projekt, der Post hat mir ebenfalls sehr geholfen. Aus reiner Neugierde würde es mich sehr interessieren, wie du aus dem Kamerabild selbst die Perspektive berechnest. Mit welchen Algorithmen / Ansätzen arbeitest du da? |
||
|
www.illusion-games.de
Space War 3 | Space Race | Galaxy on Fire | Razoon Gewinner des BCC #57 User posted image |
||
|
|
Vertex |
Antworten mit Zitat |
|---|---|---|
|
Hallo Firstdeathmaker,
wollte das eigentlich als Artikel für die neue PBM-Ausgabe entwickeln, aber ich glaube die Zeit fehlt dafür. Hier die Schritte, um vom Rohbild (Webcam) zur MV-Matrix zu gelangen, die dann in OpenGL eingesetzt werden kann. Ziel ist es, ein orangenes Quadrat (im Beispielbild ist es aber ein Rechteck) zu erkennen, dass die projezierte X-Y-Ebene in OpenGL darstellt. 1. Farbraum-Transformation von RGB nach HSV Um die orangenen Flächen im Bild zu erkennen, muss zunächst in den HSV-Farbraum transformiert werden. Der Hue(H)-Kanal enthält die Farben unabhängig von Helligkeit und Sättigung. Orange liegt in etwa bei [0°, 40°]. Ich markiere (= 1-Bit-Maske) Pixel, die (0° <= h <= 40°, s > 40%, v >28%) erfüllen, also orange sind, und ein Mindestmaß an Sättigung und Helligkeit erfüllen. 2. Lücken schließen mittels morphologischen Closing Bei verrauschten Bildern passiert es, dass die orangenen Flächen "durchlöschert sind", weil einige Pixel die Bedingung nicht erfüllen. Um die Lücken zu schließen, wende ich die morphologische Operation "Closing" an. Closing besteht aus Dilatation (Erweitern von Flächen) und Erosion (Abtragen von Flächen). Für 1-Bit Bilder ist das recht einfach: Dilatation ist ein lokaler Maximum-Filter. Er erweitert Flächen und schließt gleichzeitig Lücken. Erosion ist ein Minimum-Filter, der die Kontur wieder verkleinert, d. h. auf Originalgröße bringt, dabei aber die geschlossenen Lücken nicht "anfasst". Bei meiner Handy-Kamera ist Closing nicht nötig gewesen, bei meiner 320 x 240 Pixel Kamera vom Laptop aber schon (abends entstanden sehr verrauschte Bilder). Da hat ein 7 x 7 Pixel großen Minimum- und Maximum-Filter-Kern alles geschlossen. Das Resultat nach Schritt 1 und 2 (grün hervorgehoben die und geschlossene 1-Bit-Maske): 3. Größte Region finden Wie im Bild zu sehen ist, gibt es noch andere orangene Flächen, die auch erkannt wurden. Unter der Annahme, dass man das orangene Quadrat sehr nah in die Kamera hält, sollte die zugehörige Region/Fläche am größten sein. Deswegen bilde ich für die komplette Maske Regionen und suche dann die größte Region, d. h. die mit den meisten Pixeln. Da ich den Namen der Methode nicht kenne, hier der Algorithmus zur Regionenbildung: Code: [AUSKLAPPEN] int region[][] = new int[width - 1][height - 1] // RegionenNr an der Stelle (x, y)
map<Integer, Integer> remap = new HashMap<Integer, Integer>() // Remapping der RegionenNr int currentRegion = 1; // Ränder werden nicht betrachtet for (int x = 1; x < width; x++) { for (int y = 1; y < height; y++) { if (picture[x][y] == 0) // Ist an der Stelle (x,y) ein Pixel? continue; left = region[x - 1][y]; // RegionenNr des linken Nachbarpixels top = region[x, y - 1]; // RegionenNr des oberen Nachbarpixels if (left != 0 && left == top) // gehören left und top zur selben RegionenNr? region[x][y] = left; else if (left != 0 && top == 0) // ist nur left gesetzt? region[x][y] = left; else if (left == 0 && top != 0) // ist nur top gesetzt? region[x][y] = top; else if (left == 0 && top == 0) { // neue RegionenNr? currentRegion++; region[x][y] = currentRegion; } else if (left != 0 && left != top) { // haben left und top untersch. RegionenNr? if (left < top) { // hat left kleinere RegionenNr als top? remap.put(top, left); // top wird zu left remappt region[x][y] = left; } else if (top < left) { // hat top kleinere RegionenNr als left? remap.put(left, top); // left wird zu top remappt region[x][y] = top; } } } } // Remapping der RegionenNr for (int x = 0; x < width; x++) { for (int y = 0; y < height; y++) { currentRegion = region[x][y]; while (remap.containsKey(currentRegion)) { currentRegion = remap.get(currentRegion); } region[x][y] = currentRegion; } } picture[x,y] ist die 1-Bit-Maske, die alle orangenen Pixel markiert. region[x][y] ist die Regionen-Nummer an Position (x,y). 4. Kontur der orangenen Region erzeugen Im Schritt 3 kommt eine weiße Fläche heraus. Von ihr braucht man aber nur die Kontur. Habe das schnell mit Gimp berechnet. Ein Algorithmus für ein 1-Bit-Bild ist aber sich schnell entwickelt, oder man wendet den Sobel- bzw. Laplace-Filter an. Resultat nach der Kontur-Bildung: 5. Linien finden mittels Hough-Transformation Das 1-Bit-Bild wird in den Hough-Raum transformiert. Das bedeutet, für jeden Pixel der Kontur wird berechnet, auf welchen Geraden (alpha, distance) dieser liegt. Dabei ist alpha der Winkel des Normalen-Vektors, und Distance der Abstand zum Null-Punkt. Es werden dann im Houghraum Häufungspunkte gesucht, d. h. die Geraden, auf denen besonders viele Pixel liegen. Hier im Bild sieht man links den Hough-Raum (X-Achse entspricht Alpha, Y-Achse Distance) mit den vier Häufungspunkten und rechts die dazugehörigen Geraden: 6. Schnittpunkte der vier Geraden finden Die Schnittpunkte sind die vier Kanten des projezierten Quadrats. Weitere Schritte All das war nun Vorverarbeitung. Meine Idee ist nun folgendes: Gegeben sei ein 1 x 1 großes Quadrat auf X-Z-Ebene. Dieses Quadrat wird beschrieben durch zwei Vektoren u = (1,0,0,1) und v = (0,0,-1,1) Gegeben sei ebenfalls eine feste Projektions-Matrix mit Seitenverhältnis 640 zu 480 und einen FOV-Y-Winkel von 45°: gluPerspective(45.0, 640.0 / 480.0, 0.1, 100.0). Gesucht ist nun eine Model-View-Matrix M, sodass das projezierte Quadrat mit dem des Webcam-Bildes übereinstimmt. Gedanklich muss dazu die "OpenGL-Kamera" verschoben und rotiert werden. Diese Information (Rotation und Translation) steckt in der M-Matrix, die gesucht wird: Hier ein eine M-Matrix, die in etwa das Quadrat so transformiert, dass es projeziert mit dem Webcam-Bild übereinstimmt: Code: [AUSKLAPPEN] SuperStrict
Framework brl.glmax2d GLGraphics(640, 480, 0) glClearColor(0.0, 0.0, 0.0, 1.0) glClear(GL_COLOR_BUFFER_BIT) glViewport(0, 0, 640, 480) glMatrixMode(GL_PROJECTION) glLoadIdentity() gluPerspective(45.0, 640.0 / 480.0, 0.1, 100.0) Global tx : Float, ty : Float, tz : Float = -10.0 Global pitch : Float, yaw : Float, roll : Float pitch= 27.2000675 yaw= 13.1000137 roll= 0.000000000 tx= 0.799999952 ty= -2.49999976 tz= -4.59999609 While Not KeyDown(KEY_ESCAPE) glMatrixMode(GL_MODELVIEW) glLoadIdentity() If KeyDown(KEY_A) Then pitch :+ 0.1 If KeyDown(KEY_Y) Then pitch :- 0.1 If KeyDown(KEY_S) Then yaw :+ 0.1 If KeyDown(KEY_X) Then yaw :- 0.1 If KeyDown(KEY_D) Then roll :+ 0.1 If KeyDown(KEY_C) Then roll :- 0.1 If KeyDown(KEY_RIGHT) Then tx :+ 0.1 If KeyDown(KEY_LEFT) Then tx :- 0.1 If KeyDown(KEY_UP) Then ty :+ 0.1 If KeyDown(KEY_DOWN) Then ty :- 0.1 If KeyDown(KEY_F) Then tz :- 0.1 If KeyDown(KEY_V) Then tz :+ 0.1 glRotatef(pitch, 1.0, 0.0, 0.0) glRotatef(yaw, 0.0, 1.0, 0.0) glRotatef(roll, 0.0, 0.0, 1.0) glTranslatef(tx, ty, tz) glClear(GL_COLOR_BUFFER_BIT) glBegin(GL_LINES) glColor3f(0.0, 0.0, 1.0) glVertex4f(0.0, 0.0, 0.0, 1.0) glVertex4f(1.0, 0.0, 0.0, 1.0) ' = u (blau) glColor3f(1.0, 0.0, 0.0) glVertex4f(0.0, 0.0, 0.0, 1.0) glVertex4f(0.0, 0.0, -1.0, 1.0) ' = v (rot) glEnd() Flip() Wend End Gegeben sind die projezierten Screen-Koordinaten aus dem Webcam-Bild u'', v'' und die "unprojezierten" Original-Vektoren u = (1,0,0,1) und v = (0,0,-1,1). Die Projektion von u nach u''' und v nach v''' bilden mit der unbekannten M-Matrix ein (nicht-lineares) Gleichungssystem: u'' = P x M x u u'' = u'' / u''w u'''x = (640 * (u''x + 1))/2 u'''y = (480 * (u''y + 1))/2 v'''x = (640 * (v''x + 1))/2 v'''y = (480 * (v''y + 1))/2 Zur Erinnerung: u''', v''' sind gegeben durch das Webcambild, P ist gegeben durch gluPerspective, und u und v sind gegeben. Die Unbekannte ist hier die Matrix M, deren elemente m_ij durch das Gleichungssystem zu bestimmen sind. Da aber die Projektion keine lineare Transformation (wegen u'' = u''/u''w) ist, ist das auch kein lineares Gleichungssystem. Es muss also bspw. ein mehrdimensionales Newton-Verfahren her. Zudem sind nur 4 Gleichungen für 4*4 = 16 Unbekannte m_ij gegeben. Die Anzahl verringert sich aber auf 12, da die letzte Zeile von M Konstant ist. Das heißt, einige Elemente m_ij sind frei wählbar. Ich glaube, bei den Profi-Frameworks, wie OpenCV, heißt das finden der M-Matrix "Camera-Calibration": Habe es noch nicht gelesen, aber hier der Wiki-Eintrag dazu: http://opencv.willowgarage.com...ction.html Um nun den AR-Effekt zu erhalten, kann die gelöste M-Matrix mittels glLoadMatrix geladen werden. Man zeichnet dann das Webcam-Bild in den Hintergrund und darüber ein 3D-Mesh. Naja, mir fehlt die Zeit, um das Gleichungssystem aufzustellen und dann noch das mehrdimensionale Newton-Verfahren zu implementieren Ciao Olli |
||
| vertex.dreamfall.at | GitHub | ||
|
|
Firstdeathmaker |
Antworten mit Zitat |
|---|---|---|
|
Ok, so ungefähr ist auch mein Ansatz. Bei mir geht es allerdings darum, ein 3D-Objekt zu tracken, weshalb bei mir zunächst eine andere Technik zum Einsatz kommt um Punktkorrespondenzen zu ermitteln.
Ich sitze gerade an dem Punkt, wo man eine Menge Punktkorrespondenzen (3D <-> 2D Punkte) hat und daraus die MODELVIEW-Matrix ermitteln möchte. In einem Paper habe ich dazu gelesen, dass man die grosse Matrix des Gleichungssystemes mit den 12 Gleichungen einfach mittels einer SVD (Singularitätswertzerlegung) in drei Teilmatrizen zerlegen kann, sodass: A = U * S * V^(T) Und die letzte Spalte von V wäre die gesuchte Lösung. Die Rotation und Translation der Modelviewmatrix ergeben sich dann aus skalierten Werten dieser Lösung. Quelle: IGD Fraunhofer Augmented Reality VL Ab Seite 43 bis Seite 50 Nur irgendwie steckt bei mir noch der Wurm drin. Was ich bisher gemacht habe is, dass ich dieses Verfahren implementiert habe und es dann erst einmal testen wollte. Also habe ich mir eine kleine Testbench geschrieben, die zufällig 3D-Punkte erstellt, diese mit der hier beschriebenen Methode in 2D-Bildschirmpunkte transferiert und dann 6 dieser Punktkorrespondenzen an meinen Algorithmus übergibt. Eigentlich müsste ich ja dann eine Teilmatrix meiner Modelview-Matrix als Ergebnis erhalten (eine 4x3 Matrix, also ohne die letzte triviale Zeile). Diese müsste unabhängig von den Werten der zufällig gewählten Eingangspunkten sein. Das scheint sie jedoch nicht zu sein, sie ändert sich mit jedem Aufruf. Eines meiner Probleme besteht glaube ich darin, dass errechnete Lösung ja Freiheitsgrade besitzt und ich nicht weis, wie ich den Skalar wählen soll damit meine Lösung passt. Ein weiteres Problem ist, dass in dem Paper von einer einfachen Kameralinse ausgegangen wird, und die nichtlinearen Verzerrungen weggelassen werden. Edit: Sehr interessant neben OpenCV ist auch FastCV von Qualcomm: FastCV |
||
- Zuletzt bearbeitet von Firstdeathmaker am Mi, Nov 02, 2011 14:23, insgesamt einmal bearbeitet
|
|
Vertex |
Antworten mit Zitat |
|---|---|---|
|
Wenn ich Dich richtig verstehe, willst Du die Rotation und Translation eines aufgenommenen Objekts bestimmen, bzw. die Translation und Rotation der Kamera, wenn das Objekt fest am Ursprung steht. Dazu kennst Du n Punkte im Object-Space und hast durch's Tracking die (korrespondierenden?) Screen-Koordinaten.
In dem PDF ist die Projektion von den Object-Space-Koordinaten (X^C, Y^C, Z^C) in die Screen-Koordinaten (X, Y): Code: [AUSKLAPPEN] | X^~ | | fx s cx | | X^C |
| Y^~ | = | 0 fy cy |*| Y^C | | Z^~ | | 0 0 1 | | Z^C | d. h. X^~ = fx*X^C + s*Y^C + cx*Z^C Y^~ = fy*Y^C + cy*Z^C Z^~ = Z^C | X | = | X^~ / Z^~ | | Y | | Y^~ / Z^~ | d. h. X = (fx*X^C + s*Y^C + cx*Z^C) / Z^C Y = (fy*Y^C + cy*Z^C) / Z^C <==> X = (fx*X^C + s*Y^C ) / Z^C + cx Y = (fy*Y^C) / Z^C + cy Um mit der selben Projektion in OpenGL zu arbeiten, müsste man erst einmal die Projection-Matrix erzeugen. Selbst da habe ich schon meine Probleme. Nehme wir bspw. folgene Projection-Matrix: Code: [AUSKLAPPEN] | fx s -1 0 |
P = | 0 fy -1 0 | | 0 0 -1 0 | | 0 0 1 0 | wenn v = (X^C, Y^C, Z^C, 1), dann ist v'': Code: [AUSKLAPPEN] v'' = P x v
v''x = fx*X^C + s*Y^C - 1*Z^C v''y = fy*Y^C - 1*Z^C v''z = -1*Z^C v''w = Z^C nach der "Normierung" von v'' durch v'' = v''/v''w ergibt das: Code: [AUSKLAPPEN] v''x = (fx*X^C + s*Y^C)/Z^C -1
v''y = (fy*Y^C)/Z^C - 1 v''z = (-Z^C)/Z^C = -1 v''w = (Z^C)/Z^C = 1 Das sind die homogonen Koordinaten, die dann in die Windows-Koordinaten transformiert werden (winX, winY, winZ): Code: [AUSKLAPPEN] winX = view(0) + (view(2)*(v''x + 1)) / 2
winY = view(1) + (view(3)*(v''y + 1)) / 2 winZ = (v''z + 1) / 2 Wählt man: Code: [AUSKLAPPEN] view(0) = cx
view(1) = cy view(2) = 2 view(3) = 2 Bekommt man: Code: [AUSKLAPPEN] 2 * ((fx*X^C + s*Y^C)/Z^C -1 + 1)
winX = cx + --------------------------------- 2 winX = cx + (fx*X^C + s*Y^C)/Z^C 2 * ((fy*Y^C)/Z^C - 1 + 1) winY = cy + -------------------------- 2 winY = cy + (fy*Y^C)/Z^C -1 + 1 winZ = ------ 2 winZ = 0 Man sieht winX, winY stimmen mit den Screen-Koordinaten X, Y aus dem PDF überein. Der Knackpunkt ist allerdings winZ das nicht mit Z aus dem PDF übereinstimmt. Man kann die Projection-Matrix drehen und wenden wie man will, durch die "Normalisierung" von v'' kürzt sich stets Z^C heraus. Dann verstehe ich Seite 49 noch nicht. Die P-Matrix ist quasi die Modelview-Matrix? Enthält also Rotation und Translation. Das heißt, P ist gesucht und muss durch das Gleichungssystem auf Seite 49 bestimmt werden. In das Gleichungssystem fließen n gegebene Punkte Qi ein? Um das zu lösen, kommt die Methode SVD zum Einsatz? Da ich nur die Hälfte verstehe, kann ich Dir da also nicht so recht helfen. Aber vllt. hilft Dir noch folgender Link, den ich zum Begriff DLT gefunden habe: http://www.kwon3d.com/theory/dlt/dlt.html Ciao Olli |
||
| vertex.dreamfall.at | GitHub | ||
|
|
Firstdeathmaker |
Antworten mit Zitat |
|---|---|---|
|
Hmm, danke für deine Mühe! Werd mir das nochmal in Ruhe anschauen müssen.
Zu deiner Frage zur Seite 49: Die Lösungen der Unbekannten Modelview-Matrix sollen angeblich in der letzten Spalte der V-Matrix stehen, Merke: die V-Matrix ist eine 12x12 Matrix, die letzte Spalte umfasst also 12 Einträge. Diese sollen quasi = dem Vektor P sein in welchem die Modelview-Matrix gespeichert ist (bzw. nur ein Teil davon, die unterste Zeile wird ja bei dem PDF nicht einmal erwähnt...) Ich bin mir sowieso nicht ganz sicher ob der Ansatz hier klappen kann, weil sie ja schon die intrinsischen Kameraparameter durch eine Einheitsmatrix ersetzen. Edit: Danke für den Link! Edit2: Mir sind bei deinem Posting noch ein paar Fragen aufgekommen: Code: [AUSKLAPPEN] | fx s -1 0 |
P = | 0 fy -1 0 | | 0 0 -1 0 | | 0 0 1 0 | wie kommst du auf diese Matrix? Im Paper steht eine +1 in der unteren rechten Ecke der oberen linken 3x3 Matrix. Zitat: Man sieht winX, winY stimmen mit den Screen-Koordinaten X, Y aus dem PDF überein.
Wo im paper sieht man das? Im paper wird nur der lineare Zusammenhang zwischen den homogenen X,Y Koordinaten und den Objektkoordinaten im Kameraraum (X^c, Y^c, Z^c)) benutzt, um über das Kreuzprodukt die Bedingungen für ein lineares, homogenes Gleichungssystem aufzustellen, oder? |
||
|
www.illusion-games.de
Space War 3 | Space Race | Galaxy on Fire | Razoon Gewinner des BCC #57 User posted image |
||
|
|
Vertex |
Antworten mit Zitat |
|---|---|---|
|
Sorry, hatte Deinen zweiten Edit übersehen...
Firstdeathmaker hat Folgendes geschrieben: Edit2: Mir sind bei deinem Posting noch ein paar Fragen aufgekommen: Code: [AUSKLAPPEN] | fx s -1 0 |
P = | 0 fy -1 0 | | 0 0 -1 0 | | 0 0 1 0 | wie kommst du auf diese Matrix? Im Paper steht eine +1 in der unteren rechten Ecke der oberen linken 3x3 Matrix. Zitat: Man sieht winX, winY stimmen mit den Screen-Koordinaten X, Y aus dem PDF überein.
Wo im paper sieht man das? Im paper wird nur der lineare Zusammenhang zwischen den homogenen X,Y Koordinaten und den Objektkoordinaten im Kameraraum (X^c, Y^c, Z^c)) benutzt, um über das Kreuzprodukt die Bedingungen für ein lineares, homogenes Gleichungssystem aufzustellen, oder? Auf Seite 43 steht, dass die Projektion sich durch zweit Operationen ausdrücken lässt: Erste Operation (X^~, Y^~, Z^~)^T = K x (X^C, Y^C, Z^C)^T: Code: [AUSKLAPPEN] | X^~ | | k11 k12 k13 | | X^C |
| Y^~ | = | k21 k22 k23 |*| Y^C | | Z^~ | | k31 k32 k33 | | Z^C | Zweite Operation: Code: [AUSKLAPPEN] | X | = | X^~ / Z^~ |
| Y | | Y^~ / Z^~ | (Edit: Durch die zweite Operation ist die Projektion keine lineare Transformation!) Die Matrix K wird von Seite 43 auf Seite 44 geändert in: Code: [AUSKLAPPEN] | fx s cx |
K = | 0 fy cy | | 0 0 1 | Ich habe versucht, die beiden Operationen aus der PDF mit OpenGL nachzubilden. Dazu habe ich eine Projektionsmatrix P und den Viewport-Vektor (view(0), view(1), view(2), view(3)) so aufgebaut, dass die PDF-Projektion von (X^C, Y^C, Z^C) nach (X, Y) übereinstimmt mit der OpenGL-Projektion von (X^C, Y^C, Z^C) nach (winX, winY). Es musste also gelten: Code: [AUSKLAPPEN] | X | = | winX |
| Y | | winY | Die Lösung dafür ist: Code: [AUSKLAPPEN] | fx s -1 0 |
P = | 0 fy -1 0 | | 0 0 -1 0 | | 0 0 1 0 | view(0) = cx view(1) = cy view(2) = 2 view(3) = 2 Das ist wohlgemerkt eine von mehreren Lösungen. Was hat das nun für einen Sinn? Die PDF beschreibt ein Verfahren, um die ModelView-Matrix M=[R|t] zu berechnen. Lädt man nun P als Projection-Matrix, die berechnete Modelview-Matrix M in OpenGL und zeichnet damit die Korrespondenzpunkte, dann sollten die projezierten Punkte mit dem Webcambild übereinstimmen. |
||
| vertex.dreamfall.at | GitHub | ||
|
|
Firstdeathmaker |
Antworten mit Zitat |
|---|---|---|
|
Danke für deine Antwort!
Hmm, vielleicht habe ich ja was grundlegendes noch nicht verstanden... Ich dachte die OpenGL-Projektion lautet folgendermassen: v = Ursprünglicher Vektor Multiplikation mit der Modelview-Matrix, transferiert den Vektor v ins Koordinatensystem der Kamera -> v', bzw. Vc mit {Xc,Yc,Zc,Wc} v' = M * v Multiplikation mit der Projection-Matrix, bildet die Koordinaten auf die Bildebene der Kamera ab: v'' = P * v' mit v'' = Vp mit {Xp, Yp, Zp, Wp} Bis hierhin ist der Vektor noch homogen. Für eine perspektivische Projektion wird jetzt noch durch die Tiefe geteilt: v''' = v'' / Zp(v'') Danach müsste dann noch mit Hardware-Bildschirmauflösungen Addiert / Multipliziert werden damit die Projektion von [-0.5,0.5] -> z.B. [0,800] geht. In dem Paper hingegen wird mit der Kamermatrix K und der Pose M gerechnet. K ist dabei ein Ausschnitt der OpenGL Projection-Matrix P und M ein Ausschnitt der Modelview-Matrix (jeweils der obere linke). Wenn ich jetzt deine Lösung nehme, und P * View Rechne, erhalte ich: {Cx-2, Cy-2, -2 2}. Inwiefern das die im Paper genannte Projektion mit Teilung nachahmt verstehe ich nicht... Mein Ansatz war bisher der, dass ich die Projektionsmatrix aus dem Paper genommen habe und mit diesem Artikel verglichen habe. Die vereinfachte Projectionsmatrix K aus dem paper lautet ja: Code: [AUSKLAPPEN] | 1 0 0 | | 0 1 0 | | 0 0 1 | Die aus dem OpenGL-Artikel: 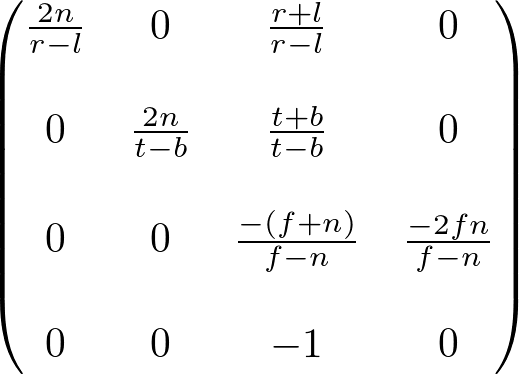
Wenn ich das jetzt als Ausschnitt der oberen linken Ecke der Projektionsmatrix aus dem OpenGL-Artikel nehme und die Gleichungen auflöse (mit n=1), erhalte ich: 2 / ( r - l ) = 1 2 / ( t - b ) = 1 ( r + l ) / ( r - l ) = 0 ( t + b ) / ( t - b ) = 0 - ( f + 1 ) / ( f - 1) = 1 Was zu einem Fehler führt ( - l = 2 + l -> 0 = 2 -> fehler) Also irgendwas an meinem Wissen ist falsch. |
||
|
www.illusion-games.de
Space War 3 | Space Race | Galaxy on Fire | Razoon Gewinner des BCC #57 User posted image |
||
|
|
mpmxyz |
Antworten mit Zitat |
|---|---|---|
|
Code: [AUSKLAPPEN] v''' = v'' / Zp(v'')
Hier ist etwas falsch, da in OpenGL durch die w-Koordinate geteilt wird, um die Perspektive zu erzeugen. Die Z-Koordinate wird hingegen unter Anderem für den Tiefenpuffer verwendet. (Irgendetwas war auch mit der Interpolation zwischen den Dreieckspunkten.) Eine Frage: Hast du dich schon darum gekümmert, die Kamera-/Kalibriermatrix deiner Kamera zu bestimmen? Ohne die kann die Berechnung aus der PDF nicht angewandt werden. Zitat: Im folgenden: vereinfachtes
Kameramodell Hierzu: Bildpunkte können vorher mit K^-1 multipliziert werden. Es gibt nun zwei Wege, das zu realisieren: 1. Du nutzt den Rechenweg aus der PDF und zerlegst dann die entstehende 3x4-Matrix in die Kalibriermatrix und die Modelviewmatrix. 2. Du bestimmst die Kalibriermatrix über ein anderes Verfahren und rechnest sie über K^-1 aus den Bildpunkten heraus. Dann bekommst du direkt die Modelviewmatrix heraus. mfG mpmxyz |
||
|
Moin Moin!
Projekte: DBPC CodeCruncher Mandelbrot-Renderer |
||
|
|
Vertex |
Antworten mit Zitat |
|---|---|---|
|
Firstdeathmaker hat Folgendes geschrieben: Danke für deine Antwort!
Hmm, vielleicht habe ich ja was grundlegendes noch nicht verstanden... Ich dachte die OpenGL-Projektion lautet folgendermassen: v = Ursprünglicher Vektor Multiplikation mit der Modelview-Matrix, transferiert den Vektor v ins Koordinatensystem der Kamera -> v', bzw. Vc mit {Xc,Yc,Zc,Wc} v' = M * v Genau, in OpenGL heißt v "Objektkoordinaten" und v' heißt "Eye-Koordinaten". Im Paper ist v = (X^W, Y^W, Z^W) (World-Koordinaten) und v' = (X^C, Y^C, Z^C) (Camera-Koordinaten). Firstdeathmaker hat Folgendes geschrieben: Multiplikation mit der Projection-Matrix, bildet die Koordinaten auf die Bildebene der Kamera ab:
v'' = P * v' mit v'' = Vp mit {Xp, Yp, Zp, Wp} Was Du mit dem Index "p" hier meinst, weiß ich nicht. In OpenGL bildet v'' die Clip-Koordinaten. Im Paper ist v'' = (X^~, Y^~, Z^~). Firstdeathmaker hat Folgendes geschrieben: Bis hierhin ist der Vektor noch homogen. Für eine perspektivische Projektion wird jetzt noch durch die Tiefe geteilt:
v''' = v'' / Zp(v'') Wie mpmxyz bereits sagte, verstehe ich das hier auch nicht. In OpenGL muss v'' durch die w-Komponente von v'' geteilt werden: v'' = v''/v''w (Du willst durch die z-Komponente dividieren). Der neue v'' Vektor heißt in OpenGL "Normalized Device-Koordinaten". Hier liegt wohlmöglich Dein Fehler/Verständnisproblem. Im Paper wird v'' durch die z-Komponente von v'' geteilt, in OpenGL wird aber durch die w-Komponente geteilt (was Du auch nicht ändern kannst). Firstdeathmaker hat Folgendes geschrieben: Danach müsste dann noch mit Hardware-Bildschirmauflösungen Addiert / Multipliziert werden damit die Projektion von [-0.5,0.5] -> z.B. [0,800] geht.
Jup, in OpenGL sind das die sogenannten "Window-Koordinaten". Im Paper entspricht das (X, Y). Firstdeathmaker hat Folgendes geschrieben: In dem Paper hingegen wird mit der Kamermatrix K und der Pose M gerechnet. K ist dabei ein Ausschnitt der OpenGL Projection-Matrix P und M ein Ausschnitt der Modelview-Matrix (jeweils der obere linke).
Wie gesagt, hier liegt der Fehler. Wenn Du einfach die K und M Matrizen in OpenGL als P und M Matrizen nimmst, dann wird in OpenGL nicht durch die z-Komponente sondern durch die w-Komponente teilen. Deswegen muss P so umgestellt werden, dass die w-Komponente den Wert der z-Komponente annimmt. Sieh Dir bspw. mal Code: [AUSKLAPPEN] | 1 0 0 0 |
A = | 0 1 0 0 | | 0 0 1 0 | | 0 0 1 0 | an. Mit dieser Matrix kann man die z-Komponente in die w-Komponente kopieren: Code: [AUSKLAPPEN] | 1 0 0 0 | | ux | | ux |
| 0 1 0 0 | x | uy | = | uy | | 0 0 1 0 | | uz | | uz | | 0 0 1 0 | | uw | | uz | Und das ist der Trick bei meiner P-Matrix. Es wird die z-Komponente in die w-Komponente kopiert. OpenGL teilt durch die w-Komponente und damit durch die urspr. z-Komponente. Noch was zu meinem AR-Projekt: Mit folgendem Gleichungssystem komme ich an die ModelView-Matrix M: Code: [AUSKLAPPEN] | width*((p11*m11 + p11*m14)/(-m31 - m34) + 1)/2 - uWinX = 0 |
| height*((p22*m21 + p22*m24)/(-m31 - m34) + 1)/2 - uWinY = 0 | | width*((p11*m13 + p11*m14)/(-m33 - m34) + 1)/2 - vWinX = 0 | | height*((p22*m23 + p22*m24)/(-m33 - m34) + 1)/2 - vWinY = 0 | wobei P = (pij ) die OpenGL-Projection-Matrix ist, width = view(3), height = view(4). (uWinX, uWinY) sowie (vWinX, vWinY) sind die zwei Windows-Koordinaten, die ich aus dem Webcambild entnehme. Die ModelView-Matrix M = (mij) ist: Code: [AUSKLAPPEN] | m11 m12 m13 m14 |
M = | m21 m22 m23 m24 | | m31 m32 m33 m34 | | 0 0 0 1 | Man sieht, 12 Unbekannte aber nur 4 Gleichungen. Dennoch konnte Octave das Gleichungssystem lösen, und ich bekam eine M-Matrix die, perfekt in das Webcambild rein passt. Wenn ich das Gleichungssystem automatisch lösen kann (mittels Newton-Raphson für ein nichtlineares Gleichungssystem), dann poste ich mal wieder Bilder rein. Ciao Olli |
||
| vertex.dreamfall.at | GitHub | ||
Übersicht
 BlitzMax, BlitzMax NG
BlitzMax, BlitzMax NG  Allgemein
Allgemein
Powered by phpBB © 2001 - 2006, phpBB Group
