2D Physik für Spiele
Übersicht BlitzBasic
BlitzBasic  FAQ und Tutorials
FAQ und Tutorials|
|
coolo |
Antworten mit Zitat |
|---|---|---|
| Sehr schön, freue mich auf mehr! Werde mich dann darin einarbeiten. | ||
|
http://programming-with-design.at/ <-- Der Preis ist heiß!
That's no bug, that's my project! "Eigenzitate sind nur was für Deppen" -Eigenzitat |
||
FWeinbehemals "ich" |
Antworten mit Zitat |
|
|---|---|---|
|
Sehr schönes Tutorial, ich habe mich auch mal etwas Informiert und dieses Tutorial bzw. diese Beschreibung gefunden sie beschreibt die Implementation von SAT, dort sind auch Beispiele in Flash zu finden.
Dort wird das ganze zwar nicht sogut erklärt, wie hier, doch finde ich die Beispiele dort sehr anschaulich. Klick Danke für dieses Super Tutorial. Ich bin mir aber nicht sicher ob das ganze auch Schnell genug für eine Echtzeitberechnung ist, da das ganze doch schon ziemlich Komplex wird. mfg ich |
||
|
"Wenn die Menschen nur über das sprächen, was sie begreifen, dann würde es sehr still auf der Welt sein." Albert Einstein (1879-1955)
"If you live each day as if it was your last, someday you'll most certainly be right." Steve Jobs |
||
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
Oh, es ist Echtzeitfähig, wie man sich hier überzeugen kann |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
FWeinbehemals "ich" |
Antworten mit Zitat |
|
|---|---|---|
|
Da hast du das ganze doch auch nach, lass mich lügen, C Portier, ich meinte die hier im Thread angesprochen vorgehensweise, es mit Blitz2D berechnen zu lassen. Da C oder die Sprache die du Verwendet hast um die Dll zu erstellen doch sicherlicht schneller ist als BB.
mfg ich |
||
|
"Wenn die Menschen nur über das sprächen, was sie begreifen, dann würde es sehr still auf der Welt sein." Albert Einstein (1879-1955)
"If you live each day as if it was your last, someday you'll most certainly be right." Steve Jobs |
||
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
Ich habe eine Version, die pures Blitz3D ist (da ich den Code nur portiert habe auf C und nicht darin entwickelt habe), welche ich ebenfalls veröffentlicht habe.
Das ganze ist hier zu finden und es ist sehr wohl Echtzeittauglich Das reine SAT ist relativ schnell, den Grossteil der Berechnungszeit in der Demo fressen die Matrizenberechnungen, die leider benötigt werden. Auch im Beispielcode im Tutorial sieht man ja, dass das SAT bei 40 Objekten und jeder Menge Vertices und Edges trotzdem kaum Berechnungszeit frisst (läuft ja alles noch flüssig) - nur mal ausführen und sich überzeugen lassen EDIT: Ich hab mal nachgemessen; bei 390 Vertices und 730 Edges frisst die Funktion 1-2 Ms bei mir - und das, obwohl noch jedes Objekt gegen jedes Objekt getestet wird. Eine winzige Optimierung mit Rectsoverlap reduziert den Aufwand auf 0 Ms. |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
|
|
Noobody |
Antworten mit Zitat |
|---|---|---|
|
Nach gut einem halben Jahr (meine Güte, schon so lange her? Ich bin wohl ein ziemlich fauler Sack, was das Tutorial hier angeht Wir erinnern uns: Im ersten Teil des Tutorials haben wir ein System geschrieben, um Partikeln und Feder mithilfe der Verletintegration einigermassen realistisch berechnen zu lassen. Im zweiten Teil haben wir einen Kollisionscheck mithilfe des SAT geschrieben. Um richtige Kollisionen zu ermöglichen, müssen wir also 'nur' noch diese beiden Systeme irgendwie kombinieren - aber dafür benötigen wir zum Glück nicht komplizierte Matrizenrechnungen, wie anfangs von mir vermutet, sondern können das über ein wenig simple Vektorgeometrie lösen. Zuallererst müssen wir das SAT erweitern. Bisher haben wir das volle Potenzial des Algorithmus nämlich noch nicht ganz ausgenutzt; er kann nämlich noch mehr als nur feststellen, ob zwei Objekte kollidieren oder nicht. Führen wir uns nochmals kurz Kapitel zwei vor Augen: Dort haben wir die beiden Objekte jeweils auf eine Achse projiziert und geschaut, ob sich die Projektionen überlappen. Falls nicht, so kollidieren die beiden Objekte nicht. Falls die Projektionen aber überlappen, so soll sich das Programm nun merken, wie gross diese Überlappung ist. Stellen wir am Ende tatsächlich eine Kollision fest, interessiert uns die Achse, auf der nach der Projektion die geringste Überlappung stattgefunden hat, da sie uns zusätzliche Informationen über die Kollision liefert. Wenn man nämlich zwei Physikobjekte kollidieren lässt, muss man sie ja irgendwie wieder auseinanderbewegen, so dass sie nicht mehr kollidieren. Die Richtung, in der man die Objekte bewegt, ist dabei entscheidend - wir können sie nicht einfach in irgendeine Richtung bewegen, ansonsten bekommen wir Probleme mit der Verletintegration. Damit alles richtig läuft, müssen wir sie um den kürzesten Vektor bewegen, der möglich ist. Die Zeichnung verdeutlicht dies: 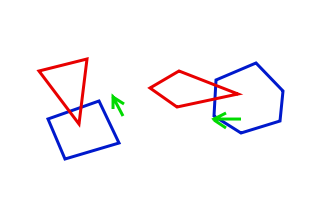
Der grüne Vektor ist jeweils der kürzeste Vektor, um den man das rote Objekt verschieben muss, damit es nicht mehr mit dem Grünen kollidiert. Diesen Vektor müssen wir zuerst noch ermitteln, aber das wird überraschend einfach. Er steht nämlich parallel zu der Achse, auf der die geringste Überlappung stattgefunden hat. Die Länge des Vektors ist gleichzeitig das Mass der Überlappung. Wenn wir das bisherige in Code umsetzen, erhalten wir folgendes: BlitzBasic: [AUSKLAPPEN] Function ProcessCollision( E1.TEntity, E2.TEntity ) Wir könnten nun einfach beide Objekte um die Hälfte dieses Vektors verschieben und wir hätten die Kollision aufgelöst; die Objekte stecken nicht mehr ineinander. Allerdings sieht das dann nicht besonders super aus - die Objekte gleiten dann nämlich nur voneinander ab und fangen sich nicht an zu drehen. Bevor wir uns mit der Lösung zu diesem Problem befassen, rufen wir uns nochmals ins Gedächtnis, dass die Verletintegration auf einzelnen Punkten basiert - nur dadurch erhalten wir Rotation. Wenn wir das ganze Objekt verschieben, stellt sich natürlich keine Drehung ein; wir müssen also einzelne Punkte der beiden Objekte verschieben. Zum Glück müssen wir nicht jeden Punkt beider Objekte einzeln berechnen, sondern müssen unser Interesse nur drei speziellen Punkten zuwenden, in der Zeichnung schwarz markiert: 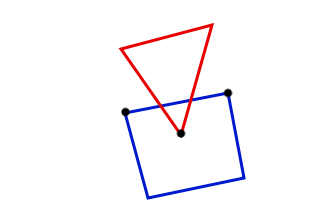
Zwei dieser Punkte gehören zum einen Objekt und bilden die penetrierte Seite, während der andere Punkt zum zweiten Objekt gehört und als penetrierter Punkt bezeichnet wird. Um relativ realistische aussehende Ergebnisse zu erreichen, müssen wir nur diese drei Punkte entsprechend dem Kollisionsvektor verschieben und wir sind fertig. Bevor wir aber die Punkte verschieben können, müssen wir die drei Punkte ja ermitteln - das ist leider nicht ganz einfach. Zuerst einmal benötigen wir die Erkenntnis, dass die Achse, auf der die kleinste Überlappung stattfindet, zu dem Objekt gehört, dass die penetrierte Seite beinhaltet. Nachdem wir also den Kollisionsvektor ermittelt haben, sorgen wir dafür, dass das Objekt, zu dem die penetrierte Seite gehört, in der Variable E2 liegt und das andere Objekt mit dem penetrierenden Punkt in E1 Nachdem das gesichert ist, beschäftigen wir uns vorerst mal mit dem einfacheren Fall, nämlich den penetrierenden Punkt zu bestimmen. Der penetrierende Punkt ist der Punkt, der am nächsten bei dem Objekt E2 liegt. Das ist durchaus logisch, da er der Punkt ist, der im zweiten Objekt drinsteckt - sehr viel näher kann man gar nicht kommen Wir müssen also irgendwie den Abstand von einem Punkt zu einem Objekt bestimmen - aber wie ist das zu bewerkstelligen? Den Mittelpunkt vom Objekt zu berechnen und dann mit dem Pythagoras zu arbeiten liefert falsche Ergebnisse, also müssen wir uns einer Formel bedienen, die auf den schönen Namen "Hessesche Normalform" hört. Die Hessesche Normalform (kurz HNF) berechnet uns den Abstand eines Punktes von einer Geraden. Diese Gerade steht senkrecht zu dem Kollisionsvektor: 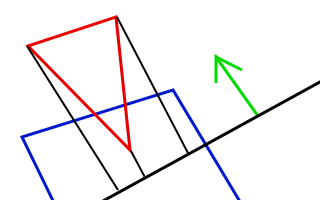
Der Kollisionsvektor ist grün gekennzeichnet, die Gerade als dicker schwarzer Strich. Mit der HNF berechnen wir nun die Abstände der Punkte von Objekt 1 zu der Gerade - wir messen quasi die Länge der dünnen schwarzen Striche auf der Abbildung. Der Punkt, dessen Abstand (oder schwarzer Strich) am kürzesten ist, ist der gesuchte penetrierende Punkt. Setzen wir das bisherige mal in Code um BlitzBasic: [AUSKLAPPEN] ;Die Hessesche Normalform hat die Gleichung X*NX + Y*NY + C Damit haben wir den penetrierenden Punkt schon ermittelt. Einfach, oder? Als nächstes folgt der ein wenig kompliziertere Fall. Wir müssen jetzt nämlich noch die penetrierte Seite bzw. die beiden Endpunkte dieser Seite ermitteln. Die penetrierte Seite hat zwei besondere Eigenschaften, die wir beachten müssen. Zum einen liegt die Seite parallel zu der Geraden, die wir zur Abstandsbestimmung verwenden. Das bedeutet, dass die Abstände der beiden Endpunkte der Seite gleich sind - da die Seite parallel zur Geraden liegt, müssen ja auch ihre beiden Endpunkte gleich weit davon entfernt sein. Zum anderen muss der penetrierende Punkt auf der penetrierten Seite liegen, wenn wir die penetrierte Seite um den Kollisionsvektor verschieben. Dies können wir einfach berechnen, indem wir den Abstand der Endpunkte der Seite von der Geraden (nachdem wir die Endpunkte um den Kollisionsvektor verschoben haben) mit dem Abstand des penetrierten Punktes vergleichen - falls es sich um die penetrierte Seite handelt, muss der Abstand gleich sein. Der entsprechende Code gestaltet sich nicht besonders kompliziert BlitzBasic: [AUSKLAPPEN] Treshold# = 0.001 ;Da Floats ungenau sind, können wir zwei Floatwerte nicht à la If A# = B# Then ... vergleichen, sondern müssen überprüfen, ob ihre Differenz unter einem Grenzwert liegt - also If A#-B# < Treshold# Then ... Nun haben wir das komplizierteste hinter uns - wir haben die drei Punkte, die von Bedeutung sind, herausgefiltert und müssen sie nun nur noch entsprechend dem Kollisionsvektor bewegen. Eine kleine Skizze zeigt, wie das ungefähr vonstatten geht 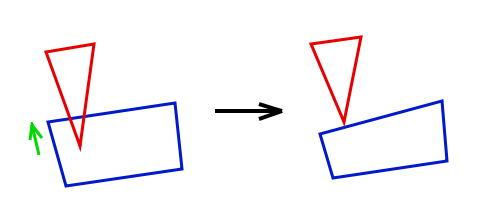
Wie wir sehen, ist der penetrierende Punkt sehr einfach zu berechnen - einfach um die Hälfte des Kollisionsvektors verschieben und fertig. BlitzBasic: [AUSKLAPPEN] LowestVertex\X# = LowestVertex\X# + CollisionVX#*0.5 Ein wenig schwieriger verhält es sich mit der penetrierten Seite; die beiden Endpunkte werden mehr oder weniger stark bewegt, je nach dem, wo auf der Seite der penetrierende Punkt liegt (siehe Skizze - die beiden Endpunkte werden nicht gleich viel nach unten bewegt). Um das noch hinzukriegen, müssen wir eigentlich nur einen Wert berechnen, wie weit der penetrierende Punkt von einem der beiden Endpunkte entfernt ist. Bei Wert 0 ist er direkt beim einen Endpunkt, bei 0.5 in der Mitte und so weiter. Dieser Wert ist mit ein wenig Vektorgeometrie schnell berechnet BlitzBasic: [AUSKLAPPEN] Ratio# = ( CollisionPX# - CollisionVX# - V1\X# )/( V2\X# - V1\X# ) Der eine Endpunkt (in der Gleichung als V2 bezeichnet) wird um den halben Kollisionsvektor multipliziert mit Ratio bewegt. Der andere Eckpunkt (V1) wiederum wird um den halben Kollisionsvektor mal 1-Ratio bewegt. Der Code gestaltet sich entsprechend simpel BlitzBasic: [AUSKLAPPEN] V1\X# = V1\X# + CollisionVX#*( 1 - Ratio# )*0.5 Das wars - fertig ist die Kollisionsberechnung! Fertig? Naja, fast. Ein kleines Problemchen mit dem Kollisionsvektor habe ich nämlich verschwiegen - je nach dem zeigt er in Richtung des Objekts E1 oder in Richtung von E2. Unser Programm rechnet aber mit der Vorraussetzung, dass der Kollisionsvektor stets nach E1 zeigt. Das können wir erreichen, indem wir folgendes unverständliche Stück Code hinzufügen BlitzBasic: [AUSKLAPPEN] Sign = Sgn( E1\CenterX#*CollAxisX# + E1\CenterY#*CollAxisY# + C# ) Um ganz ehrlich zu sein, verstehe ich nicht ganz, warum es den Else - Zweig benötigt. Den Code habe ich vor einem Dreivierteljahr geschrieben und wusste es schon damals nicht genau; ich hatte die Zeilen einfach testweise mal eingebaut und es hat funktioniert Jetzt ist die Kollision aber wirklich abgeschlossen. Definitiv ein kompliziertes Kapitel, aber nachdem das einmal fertiggestellt ist, hat man eine stabile Basis für künftige Erweiterungen - beispielsweise könnte man noch Reibung, Wasser oder elastische Federn einbauen, aber deren Implementation überlasse ich mal dem Leser Ich habe mir mal erlaubt, die bisherigen Codefetzen zusammenzufassen, damit man sich die nicht aus dem ganzen Thread zusammensuchen muss Code: [AUSKLAPPEN] Const GWIDTH = 800
Const GHEIGHT = 600 Graphics GWIDTH, GHEIGHT, 0, 2 SetBuffer BackBuffer() Const MAX_VERTICES = 64 Const MAX_EDGES = 64 Global ProjectedMin#, ProjectedMax# Global ResultX#, ResultY# Type TParticle Field X# Field Y# Field OldX# Field OldY# Field A_X# Field A_Y# Field Parent.TEntity End Type Type TConstraint Field ID Field P1.TParticle Field P2.TParticle Field Length# Field Parent.TEntity End Type Type TEntity Field VertexCount Field Vertex.TParticle[ MAX_VERTICES - 1 ] Field EdgeCount Field Edge.TConstraint[ MAX_EDGES - 1 ] Field CenterX# Field CenterY# Field MinX# Field MinY# Field MaxX# Field MaxY# End Type Const TIMESTEP# = 1 Global GRAVITY_X# = 0 Global GRAVITY_Y# = 1 Global Iterations = 10 Timer = CreateTimer( 60 ) While Not KeyHit( 1 ) Cls Counter = MilliSecs() AccumulateForces() Verlet() SatisfyConstraints() LagString$ = "Physik: " + ( MilliSecs() - Counter ) + "ms " Counter = MilliSecs() Render() LagString$ = LagString$ + "Zeichnen: " + ( MilliSecs() - Counter ) + "ms" UserInput() Color 128, 128, 128 Text 0, 0, LagString$ Flip 0 WaitTimer Timer Wend End Function UserInput() If MouseHit( 1 ) Then ;Bei Linksklick ein Dreieck erstellen Entity.TEntity = New TEntity Particle.TParticle = CreateParticle( Entity, MouseX() - 25, MouseY() - 25 ) CreateParticle( Entity, MouseX() - 25, MouseY() + 25 ) CreateParticle( Entity, MouseX() + 25, MouseY() + 25 ) CreateConstraint( Entity, Particle, After Particle ) CreateConstraint( Entity, After Particle, After After Particle ) CreateConstraint( Entity, After After Particle, Particle ) EndIf If MouseDown( 2 ) Then CreateBox( MouseX(), MouseY(), 40, 40 ) ;Bei Rechtsklick einen Würfel End Function Function AccumulateForces() ;Kräfte zusammenrechnen - bei uns nur Gravitation For Particle.TParticle = Each TParticle Particle\A_X# = GRAVITY_X# Particle\A_Y# = GRAVITY_Y# Next End Function Function Verlet() ;Bewegung der Partikel, wie im ersten Kapitel beschrieben For Particle.TParticle = Each TParticle Temp_X# = Particle\X# Temp_Y# = Particle\Y# Particle\X# = 2*Particle\X# - Particle\OldX# + Particle\A_X#*TIMESTEP#*TIMESTEP# Particle\Y# = 2*Particle\Y# - Particle\OldY# + Particle\A_Y#*TIMESTEP#*TIMESTEP# Particle\OldX# = Temp_X# Particle\OldY# = Temp_Y# Next End Function Function SatisfyConstraints() ;Diese Funktion berechnet Federn und Kollision For i = 1 To Iterations For Entity.TEntity = Each TEntity ;Für jedes Objekt den Mittelpunkt berechnen und die Bounding Box bestimmen Entity\CenterX# = 0 Entity\CenterY# = 0 MaxX# = -1000 MaxY# = -1000 MinX# = 1000 MinY# = 1000 For t = 0 To Entity\VertexCount - 1 Entity\CenterX# = Entity\CenterX# + Entity\Vertex[ t ]\X#/Entity\VertexCount Entity\CenterY# = Entity\CenterY# + Entity\Vertex[ t ]\Y#/Entity\VertexCount If Entity\Vertex[ t ]\X# > MaxX# Then MaxX# = Entity\Vertex[ t ]\X# If Entity\Vertex[ t ]\X# < MinX# Then MinX# = Entity\Vertex[ t ]\X# If Entity\Vertex[ t ]\Y# > MaxY# Then MaxY# = Entity\Vertex[ t ]\Y# If Entity\Vertex[ t ]\Y# < MinY# Then MinY# = Entity\Vertex[ t ]\Y# Next Entity\MaxX# = MaxX# Entity\MinX# = MinX# Entity\MaxY# = MaxY# Entity\MinY# = MinY# Next For E1.TEntity = Each TEntity ;Für jedes Objekt die Kollision berechnen lassen. Es wird vorher geprüft, ob sich die Bounding Boxes überlappen, um Rechenzeit zu sparen For E2.TEntity = Each TEntity If E1 <> E2 Then If RectsOverlap( E1\MinX#, E1\MinY#, E1\MaxX# - E1\MinX#, E1\MaxY# - E1\MinY#, E2\MinX#, E2\MinY#, E2\MaxX# - E2\MinX#, E2\MaxY# - E2\MinY# ) Then ProcessCollision( E1, E2 ) EndIf EndIf Next Next For Constraint.TConstraint = Each TConstraint ;Federn berechnen lassen wie im ersten Kapitel erklärt. For Particle.TParticle = Each TParticle Particle\X# = Min( Max( Particle\X#, 0 ), GWIDTH - 1 ) Particle\Y# = Min( Max( Particle\Y#, 0 ), GHEIGHT - 1 ) Next DeltaX# = Constraint\P2\X# - Constraint\P1\X# DeltaY# = Constraint\P2\Y# - Constraint\P1\Y# DeltaLength# = Sqr( DeltaX#*DeltaX# + DeltaY#*DeltaY# ) Diff# = ( DeltaLength# - Constraint\Length# )/DeltaLength# Constraint\P1\X# = Constraint\P1\X# + DeltaX#*Diff#*0.5 Constraint\P1\Y# = Constraint\P1\Y# + DeltaY#*Diff#*0.5 Constraint\P2\X# = Constraint\P2\X# - DeltaX#*Diff#*0.5 Constraint\P2\Y# = Constraint\P2\Y# - DeltaY#*Diff#*0.5 Next Next End Function Function Render() LockBuffer BackBuffer() For Entity.TEntity = Each TEntity If Entity\CenterX# >= 0 And Entity\CenterX# < GWIDTH Then If Entity\CenterY# >= 0 And Entity\CenterY# < GHEIGHT Then WritePixelFast Floor( Entity\CenterX# ), Floor( Entity\CenterY# ), $00FFFF00 ;Mittelpunkt einzeichnen EndIf EndIf Next Color 255, 0, 0 For Constraint.TConstraint = Each TConstraint Line Constraint\P1\X#, Constraint\P1\Y#, Constraint\P2\X#, Constraint\P2\Y# ;Federn zeichnen Next For Particle.TParticle = Each TParticle If Particle\X# >= 0 And Particle\X# < GWIDTH Then If Particle\Y# >= 0 And Particle\Y# < GHEIGHT Then WritePixelFast Floor( Particle\X# ), Floor( Particle\Y# ), $00FFFFFF ;Punkte zeichnen EndIf EndIf Next UnlockBuffer BackBuffer() End Function Function Min#( A#, B# ) If A# < B# Then Return A# Else Return B# End Function Function Max#( A#, B# ) If A# > B# Then Return A# Else Return B# End Function Function CreateParticle.TParticle( Parent.TEntity, X#, Y#, Mass# = 1 ) If Parent <> Null Then If Parent\VertexCount < MAX_VERTICES - 1 Then Particle.TParticle = New TParticle Particle\X# = X# Particle\Y# = Y# Particle\OldX# = X# Particle\OldY# = Y# Particle\Parent = Parent Parent\Vertex[ Parent\VertexCount ] = Particle ;Punkt zum Objekt hinzufügen Parent\VertexCount = Parent\VertexCount + 1 Return Particle EndIf EndIf End Function Function CreateConstraint.TConstraint( Parent.TEntity, P1.TParticle, P2.TParticle ) If Parent <> Null Then If Parent\EdgeCount < MAX_EDGES - 1 Then If P1 <> P2 Then Constraint.TConstraint = New TConstraint Constraint\P1 = P1 Constraint\P2 = P2 ConstraintLengthSq# = ( Constraint\P1\X# - Constraint\P2\X# )*( Constraint\P1\X# - Constraint\P2\X# ) + ( Constraint\P1\Y# - Constraint\P2\Y# )*( Constraint\P1\Y# - Constraint\P2\Y# ) Constraint\Length# = Sqr( ConstraintLengthSq# ) Constraint\Parent = Parent Parent\Edge[ Parent\EdgeCount ] = Constraint ;Seite zum Objekt hinzufügen Parent\EdgeCount = Parent\EdgeCount + 1 Return Constraint EndIf EndIf EndIf End Function Function CreateBox( X#, Y#, Width#, Height# ) Entity.TEntity = New TEntity P1.TParticle = CreateParticle( Entity, X# - Width#/2, Y# - Height#/2 ) P2.TParticle = CreateParticle( Entity, X# + Width#/2, Y# - Height#/2 ) P3.TParticle = CreateParticle( Entity, X# + Width#/2, Y# + Height#/2 ) P4.TParticle = CreateParticle( Entity, X# - Width#/2, Y# + Height#/2 ) CreateConstraint( Entity, P1, P2 ) CreateConstraint( Entity, P2, P3 ) CreateConstraint( Entity, P3, P4 ) CreateConstraint( Entity, P4, P1 ) CreateConstraint( Entity, P1, P3 ) CreateConstraint( Entity, P2, P4 ) End Function Function Dotproduct#( X1#, Y1#, X2#, Y2# ) Return X1#*X2# + Y1#*Y2# End Function Function Normalize( X#, Y# ) Length# = Sqr( X#*X# + Y#*Y# ) ResultX# = X#/Length# ResultY# = Y#/Length# End Function Function ProjectToAxis( AxisX#, AxisY#, Entity.TEntity ) Local DotP# = Dotproduct( AxisX#, AxisY#, Entity\Vertex[ 0 ]\X#, Entity\Vertex[ 0 ]\Y# ) ProjectedMin# = DotP# ProjectedMax# = DotP# For i = 1 To Entity\VertexCount - 1 DotP# = Dotproduct( AxisX#, AxisY#, Entity\Vertex[ i ]\X#, Entity\Vertex[ i ]\Y# ) If DotP# < ProjectedMin# Then ProjectedMin# = DotP# ElseIf DotP# > ProjectedMax# Then ProjectedMax# = DotP# Next End Function Function IntervalDistance#( A1#, B1#, A2#, B2# ) If A1# < A2# Then Return A2# - B1# Else Return A1# - B2# EndIf End Function Function ProcessCollision( E1.TEntity, E2.TEntity ) MinDistance# = 10000000 For i = 0 To E1\EdgeCount + E2\EdgeCount - 1 If i < E1\EdgeCount Then Edge.TConstraint = E1\Edge[ i ] Else Edge.TConstraint = E2\Edge[ i - E1\EdgeCount ] EndIf AxisX# = -( Edge\P2\Y# - Edge\P1\Y# ) AxisY# = Edge\P2\X# - Edge\P1\X# TFormNormal AxisX#, AxisY#, 0, 0, 0 AxisX# = TFormedX() AxisY# = TFormedY() ProjectToAxis( AxisX#, AxisY#, E1 ) Min# = ProjectedMin# Max# = ProjectedMax# ProjectToAxis( AxisX#, AxisY#, E2 ) Distance# = IntervalDistance( Min#, Max#, ProjectedMin#, ProjectedMax# ) If Distance# > 0 Then Return False ElseIf Abs( Distance# ) < MinDistance# Then MinDistance# = Abs( Distance# ) CollAxisX# = AxisX# CollAxisY# = AxisY# DiffX# = E1\CenterX# - E2\CenterX# DiffY# = E1\CenterY# - E2\CenterY# CollEdge.TConstraint = Edge ;Kollisionsseite zwischenmerken EndIf Next CollisionVX# = CollAxisX#*MinDistance# CollisionVY# = CollAxisY#*MinDistance# If CollEdge\Parent <> E2 Then ;Falls E2 nicht das penetrierte Objekt ist, die beiden Objekte vertauschen, so dass ersteres zutrifft Temp.TEntity = E2 E2 = E1 E1 = Temp EndIf Local C# = -E2\CenterX#*CollAxisX# - E2\CenterY#*CollAxisY# ;Konstante berechnen Sign = Sgn( E1\CenterX#*CollAxisX# + E1\CenterY#*CollAxisY# + C# ) If Sign = 1 Then ;Das hier ist eine wichtige Schutzabfrage, um sicherzustellen, dass der Kollisionsvektor immer Richtung E1 zeigt CollisionVX# = -CollisionVX# CollisionVY# = -CollisionVY# Else CollAxisX# = -CollAxisX# CollAxisY# = -CollAxisY# EndIf SmallestY# = 10000 For i = 0 To E1\VertexCount - 1 Vertex.TParticle = E1\Vertex[ i ] D# = Vertex\X#*CollAxisX# + Vertex\Y#*CollAxisY# + C# If D# < SmallestY# Then SmallestY# = D# LowestVertex.TParticle = Vertex EndIf Next Treshold# = 0.001 For i = 0 To E2\EdgeCount - 1 V1.TParticle = E2\Edge[ i ]\P1 V2.TParticle = E2\Edge[ i ]\P2 V1Y# = ( V1\X# + CollisionVX# )*CollAxisX# + ( V1\Y# + CollisionVY# )*CollAxisY# + C# V2Y# = ( V2\X# + CollisionVX# )*CollAxisX# + ( V2\Y# + CollisionVY# )*CollAxisY# + C# If Abs( V1Y# - V2Y# ) < Treshold# Then If Abs( ( V1Y# + V2Y# )/2. - SmallestY# ) < Treshold# Then Exit EndIf Next If Abs( V2\X# - V1\X# ) > Abs( V2\Y# - V1\Y# ) Then ;Das hier ist eine kleine Schutzabfrage, damit man nicht durch 0 teilt, wenn die Seite senkrecht steht Ratio# = ( LowestVertex\X# - CollisionVX# - V1\X# )/( V2\X# - V1\X# ) Else Ratio# = ( LowestVertex\Y# - CollisionVY# - V1\Y# )/( V2\Y# - V1\Y# ) EndIf V1\X# = V1\X# + CollisionVX#*( 1 - Ratio# )*0.5 V1\Y# = V1\Y# + CollisionVY#*( 1 - Ratio# )*0.5 V2\X# = V2\X# + CollisionVX#*Ratio#*0.5 V2\Y# = V2\Y# + CollisionVY#*Ratio#*0.5 LowestVertex\X# = LowestVertex\X# - CollisionVX#*0.5 LowestVertex\Y# = LowestVertex\Y# - CollisionVY#*0.5 Return True End Function Bedient wird mit der linken bzw. rechten Maustaste. Kommentare habe ich in dem Code nur spärlich gestreut, da alle Codestücke schon im Tutorial selbst ausführlich erklärt und auch kommentiert sind. Das wird voraussichtlich der letzte Teil des Tutorials sein, für Fragen stehe ich aber selbstverständlich noch zur Verfügung. |
||
| Man is the best computer we can put aboard a spacecraft ... and the only one that can be mass produced with unskilled labor. -- Wernher von Braun | ||
|
|
ComNik |
Antworten mit Zitat |
|---|---|---|
|
Herzlichen Dank nochmal! Das Modul ist fast fertig. Ich denke ich schreib auch eine DLL. |
||
| WIP: Vorx.Engine | ||
n-Halbleiter |
Antworten mit Zitat |
|
|---|---|---|
|
Also hast du doch noch Zeit gefunden. Vielen Dank dafür, dass du das geschrieben hast. Ich habe es ohne Probleme verstanden, nur mal so, dass du eine Rückmeldung bekommst. ^^ |
||
|
mfg, Calvin
Maschine: Intel Core2 Duo E6750, 4GB DDR2-Ram, ATI Radeon HD4850, Win 7 x64 und Ubuntu 12.04 64-Bit Ploing! Blog "Die Seele einer jeden Ordnung ist ein großer Papierkorb." - Kurt Tucholsky (09.01.1890 - 21.12.1935) |
||
Übersicht
 BlitzBasic
BlitzBasic  FAQ und Tutorials
FAQ und Tutorials
Powered by phpBB © 2001 - 2006, phpBB Group
