Punkt mit Vektor finden? [gelöst]

Übersicht BlitzBasic Allgemein

Neue Antwort erstellen

Midimaster

Betreff: Punkt mit Vektor finden? [gelöst]

 BeitragDo, Jan 12, 2012 12:18
Antworten mit Zitat
Benutzer-Profile anzeigen
Für unser Tram-Projekt erarbeite ich derzeit einen Straßenalgo, der automatisch Straßen generieren wird. ( https://www.blitzforum.de/upload/file.php?id=11344 )

Der Algo ist komplett 2D. Ich habe die nötigen Berechnungen bereits mit Sin/Cos gelöst, möchte aber nun (um das endlich mal zu lernen) komplett auf eine Berechnung mittels Verktor x/y/umstellen. Doch jetzt komme ich an meine Grenzen....

Gegeben ist ein Punkt M in dem sich zwei Geraden G1 und G2 kreuzen. Nun suche ich den Punkt T2, der sich auf der Gerade G2 befindet und bei dem der Abstand zu anderen Gerade G1 genau 50 ist. Der Abstandsvektor soll dabei senkrecht auf der Gerade G1 stehen. Wie macht man sowas?

ein Bild:user posted image

Die Vektoren V1 zu G1 und V2 zu G2 sind bekannt. Ebenso ist ja die Senkrechte einfach der "umgedrehte" Vektor von G1, oder?

mein Denkansantz:
1.
3 Vektoren addieren führt zum Ursprung zurück:
n*Vektor1 + 50*Vekor1umgedreht + m*Vektor2 = 0

2.
Pythagoras:
n^2 + 50^2 = m^2

Aber nützt mir das was? Wie löst man sowas?
Gewinner des BCC #53 mit "Gitarrist vs Fussballer" http://www.midimaster.de/downl...ssball.exe
  • Zuletzt bearbeitet von Midimaster am Mo, Jan 16, 2012 23:22, insgesamt einmal bearbeitet

Chrise

Betreff: Re: Punkt mit Vektor finden?

 BeitragDo, Jan 12, 2012 12:37
Antworten mit Zitat
Benutzer-Profile anzeigen
Hallo!

Wenn du mit Vektoren rechnen willst, solltest du auch bei Vektoren bleiben Wink
Da gibt es sowas wie m nicht mehr wirklich. Drückst du die Geraden als Vektoren aus
in der Form
ax
ay

G1:
+3
-4

und G2:
-2
+5

(beliebig gewählt, so kannst du auf der Geraden G2 einen Senkrechten vektor dann definieren, wenn das Skalarprodukt 0 ist. (Skalarprodukt = 0, wenn es sich um zwei senkrecht zueinander stehende Vektoren handelt)

Beispiel wäre hier:
-2*cx + +5*cy = 0
(wenn c der gesuchte Vektor ist)

ausserdem soll gelten:
sqrt(cx*cx+cy*cy) = 50
-> cx*cx+cy*cy = 2500

jetzt könntest du die erste Gleichung nach cy auflösen:
cy = 2*cx /5
und in der unteren einsetzen:
cx*cx+(2*cx/5)*(2*cx/5) = 2500
und vereinfachen:
cx²+(4/25)cx² = 2500
-> (29/25)cx² - 2500 = 0

Dann hat man es schonmal in der allgemeinen quadratischen Form (ax²+bx+c=0) und könnte diese mittels der Mitternachtsformel lösen, wenns komplizierter wäre Razz

Aber da der normale x-teil fehlt, kann man sie auch ganz einfach nach cx auflösen:
cx = sqrt(2500*25/29)

sobald man cx ausgerechnet hat, kann man cy ganz leicht mittels pythagoras ausrechnen.

Bitte korrigiert mich, wenn ich mich wo verrechnet hab, bei mir isses schon sehr spät nachts^^

EDIT: Vorraussetzung bei diesem Lösungsvorschlag ist übrigens, dass du den Schnittpunkt von dem der Vektor c ausgehen soll, bereits kennst Smile

lg Chrise
Llama 1 Llama 2 Llama 3
Vielen Dank an Pummelie, der mir auf seinem Server einen Platz für LlamaNet bietet.

Tankbuster

 BeitragDo, Jan 12, 2012 12:48
Antworten mit Zitat
Benutzer-Profile anzeigen
Ich hätte jetzt Vektor V3 (graue Linie) gebildet, der Parallel zu V1 ist, dann den Schnittpunkt zwischen V3 und V2 ausgerechnet.

Dafür brauchst du aber auch wieder Sin/Cos ....

Oder du bildest den http://de.wikipedia.org/wiki/Normalenvektor (Senkrecht), und bringst ihn im Anfangspunkt von V1 auf eine länge von 30 um V3 (graue Linie) auszurechnen. Du brauchst ja nur deren Startpunkt, der Richtungsvektor von V1 ist ja auch der von V3


Edit: Was hier vorher stand war unsinn :3
Twitter
Download Jewel Snake!
Windows|Android

darth

 BeitragDo, Jan 12, 2012 14:51
Antworten mit Zitat
Benutzer-Profile anzeigen
Hallo,

sagt dir die Hessesche Normalform (kurz HNF) etwas? Falls nein, hier Kurzanleitung:

Code: [AUSKLAPPEN]
Gegeben sei die Gerade G, mit Vektor g durch Punkt P.
Daraus folgt die Geradengleichung: A*x + B*y + C = 0
([A; B] ist der Normalvektor, wenn g = [x;y] ist [A; B] = [y; -x],
C ist Offset, wird so gemacht, dass die Gleichung für P stimmt, d.h C = -A * Px - B * Py)

Dann ist der Abstand von Punkt K zur Geraden G gegeben durch:
HNF = (A *  Kx + B * Ky + C) / sqr(A^2 + B^2)


Daraus folgen für dein Problem dann zwei Gleichungen.

1. HNF(G1, T2) = 50
2. T2 muss auf G2 liegen

Code: [AUSKLAPPEN]
(A1 * Tx + B1 * Ty + C1)/sqr(A1^2 + B1^2) = 50
A2 * Tx + B2 * Ty + C2 = 0


Das aufzulösen kann man nun entweder per Hand, oder maschinell, je nach Faulheitsgrad.

Aber das Prinzip ist ähnlich wie das was Tankbuster beschreibt, allerdings verstehe ich überhaupt nicht, wozu er Sinus und Cosinus einsetzen will :/ Und wieso er von Längen von 30 spricht ist mir auch schleierhaft. Aber trotzdem:
Du bildest eine im Abstand 50 eine Parallele G3 zu G1 und suchst dir dann einen Schnittpunkt mit G2, da du allerdings G3 nie explizit ausrechnen willst, machst dus über eine Sammlung von beliebigen Punkten die alle den gleichen Abstand zu G1 haben (ungefähre Definition einer Parallelen) und zwingst den Punkt dann über die zweite Gleichung auf die Gerade G2.

MfG,
Darth
Diese Signatur ist leer.

Tankbuster

 BeitragDo, Jan 12, 2012 15:22
Antworten mit Zitat
Benutzer-Profile anzeigen
Ich meinte natürlich 50, anstatt 30. Bin da irgendwie durcheinander gekommen.

Man könnte auch mit dem Skalarprodukt den Winkel zwischen G1 und G2 berechnen, und dann über mit den Winkelsätzen den Abstand von M bis T2 berechnen.

Aber wie man es dreht und wendet, irgendwo muss man immer einen Winkelsatz benutzen, um zu einem Ergebnis zu kommen. Man muss zwar nicht zwingend mit Sin/Cos/Tan rechnen, weil manche Formeln das irgendwie rausgekürzt haben, aber so ist es nunmal, weil die Vektoren verschiedene Ausrichtungen haben. Ist ja eigentlich logisch.
Das meinte ich damit....
Twitter
Download Jewel Snake!
Windows|Android

Midimaster

 BeitragDo, Jan 12, 2012 16:46
Antworten mit Zitat
Benutzer-Profile anzeigen
ohwe... und zunächst: Danke, mit der Bitte, es etwas langsamer zu erklären

ich glaub ich bin zu blöd für sowas...

Hier sind meine Fragen:

@crise
Zitat:
... so kannst du auf der Geraden G2 einen Senkrechten vektor...

wieso jetzt auf G2? Meine Senkrechte ist doch auf G1 und wäre der Vektor zu [+3;-4] dann nicht [-4;-3], also vertauscht und unten negativ?

Zitat:
...Vorraussetzung bei diesem Lösungsvorschlag ist übrigens, dass du den Schnittpunkt von dem der Vektor c ausgehen soll, bereits kennst...

nee, man kennt nur den Schnittpunkt der beiden Geraden bei M. Meintest du das?

@Tankbuster
Zitat:
...und bringst ihn im Anfangspunkt von V1...

meinst du damit in M?

Zitat:
Man muss zwar nicht zwingend mit Sin/Cos/Tan rechnen..

ja irgendwie muss das auch ohne gehen!

@darth
oweia, ich habs befürchtet....

Nun nennst du alle Parameter leider anders als in meiner Frage. Könntest du mir das auf mein Beispiel umsetzen. also alles was mit Gerade G1 zu tun hat mit einer 1 im Namen und alles zu G2 mit einer 2. Und die Senkrechte meinetwegen mit der 3?

Zitat:
....machst dus über eine Sammlung von beliebigen Punkten die alle den gleichen Abstand zu G1 haben (ungefähre Definition einer Parallelen) und zwingst den Punkt dann über die zweite Gleichung auf die Gerade G2....

jou mach ich! ? ? Hilfe! was? Bitte nochmal für Doofies!


Ihr seid total lieb, aber ich brauch es glaube ich noch "etwas langsamer"....
Gewinner des BCC #53 mit "Gitarrist vs Fussballer" http://www.midimaster.de/downl...ssball.exe

darth

 BeitragDo, Jan 12, 2012 18:20
Antworten mit Zitat
Benutzer-Profile anzeigen
Hallo,

manchmal frage ich mich, wieso Leute bei der geringsten Andeutung von Mathematik (oder "Komplikation" allgemein) direkt den Kopf zumachen und sich dann mit "tut mir leid, ich bin halt doof" rausreden wollen. Gerade die Mathematik ist nichts anderes als ein mehr oder weniger stures Befolgen von Anweisungen und das sollte jeder beherrschen. (Angewandte Mathematik, ich weiss, dass es kranke theoretische Mathematik gibt.)

Die Ausrede "du hast das Zeug anderst bezeichnet als ich" zeugt meiner Meinung nach von Faulheit. Dann setzt man sich halt hin und vergleicht kurz die Bezeichnungen. Das PRINZIP dahinter ist genau das gleiche, ob es jetzt g1 und g2 oder Max und Moritz heisst.

Zitat:
Bitte nochmal für Doofies!

Alright: Siehst du den Abschnitt mit den zwei Gleichungen? Alles was du tun musst, ist die nach X und Y aufzulösen (2 Glg, 2 Unbekannte -> ezpz Arithmetik!)

Aber ich will mal nicht so sein:
BlitzBasic: [AUSKLAPPEN] 
Type Vector2
	Field x#
	Field y#
End Type

Function newVector.Vector2(x#, y#)
	Local v.Vector2 = New Vector2
	
	v\x = x
	v\y = y
	
	Return v
End Function

Function getNormal.Vector2(v.Vector2)
	Return newVector(v\y, -v\x)
End Function

Function getLength#(v.Vector2)
	Return Sqr(v\x * v\x + v\y * v\y)
End Function

Graphics 800, 600, 0, 2
SetBuffer BackBuffer()

Local m.Vector2
Local g1.Vector2
Local g2.Vector2
Local d#

m = newVector(400, 300)
g1 = newVector(4, 1)
g2 = newVector(3, -1)
d = 50

Local n1.Vector2, n2.Vector2, c1#, c2#, l#, t.Vector2

While Not KeyHit(1)
	
	Oval m\x -3, m\y -3, 6, 6
	Line m\x + 100 * g1\x, m\y + 100 * g1\y, m\x - 100 * g1\x, m\y - 100 * g1\y
	Line m\x + 100 * g2\x, m\y + 100 * g2\y, m\x - 100 * g2\x, m\y - 100 * g2\y
	
	;Geradengleichung 1:
	l = getLength(g1)
	
	n1 = getNormal(g1)
	c1 = -n1\x * m\x - n1\y * m\y
		;-> n1\x * X + n1\y * Y + c1 = 0 für alle Punkte auf g1
	
	;geradengleichung 2:
	n2 = getNormal(g2)
	c2 = -n2\x * m\x - n2\y * m\y
		;-> n2\x * X + n2\y * Y + c2 = 0 für alle Punkte auf g2
	
	;Gleichung 1:
	;	(n1\x * t\x + n1\y * t\y + c1) / l = d < HNF
	;Gleichung 2:
	;	n2\x * t\x + n2\y * t\y + c2 = 0 < Pt auf G2
	
	;2 Gleichungen
	;2 Unbekannte
	
	;aufgelöst nach t\x und t\y
	det# = n1\x * n2\y - n1\y * n2\x
	
	t = New Vector2
	t\x = (d * l * n2\y - c1 * n2\y + c2 * n1\y) /det
	t\y = -(d * l * n2\x - c1 * n2\x + c2 * n1\x) /det
	
	;Resultat
	Oval t\x -3, t\y -3, 6, 6
	
	;cleanup
	Delete n1
	Delete n2
	Delete t
	
	Flip
	Cls
Wend
End


Wie man sieht ist der Punkt "über" g1, wenn man den "unter" g1 haben möchte, setzt man entweder d = -50 (das ist der einfachste Weg) oder man kehrt die Gerade g1 um (d.h g1 = [-x; -y]).

MfG,
Darth
Diese Signatur ist leer.

Midimaster

 BeitragDo, Jan 12, 2012 20:29
Antworten mit Zitat
Benutzer-Profile anzeigen
Darth, du bist ein Schatz! Dein Code macht genau, wonach ich suche. Ich werde versuchen die Wirkweise an deinem Code-Bespiel zu verstehen.

Aber Du schätzt mich total falsch ein, wenn Du meinst, Faulheit war mein Antrieb hier nochmal nachzufragen! Ich hatte heute Nacht bis 3:00 Uhr im Internet alle möglichen Seiten zu dem Thema durchgearbeitet, aber eben keinen Zusammenhang zwischen den Formeln dort und meiner Fragestellung finden können. Nun suche ich nicht nach einer "schnellen Lösung", sondern will das Ganze natürlich auch verstehen.

Die Tatsache, dass man Skalarprodukte und Vektoraddition durchführen kann, führt leider noch nicht automatisch zu dem Verständnis, was man damit nun konkret machen kann, und welche Formel in einer konkreten Fall die richtige Lösung bringt.

Zu meiner Schande muss ich zugestehen, in Mathe-Leistungskurs seinerzeit mit 14 Punkten mein Abi gemacht zu haben. Ist aber schon eine Weile (fast 30 Jahre!!!) her. Damals gab es Vektorrechung auch schon in der Schule, aber keine Computerspiele, wo man das hätte anwenden können. Es blieb doch sehr theoretisch.

Vielleicht wäre hier einmal ein Tutorial nötig, dass die Algebra aus der Sicht von Computerspielen erklärt...

Dir jedefalls herzlichen Dank. Du hast mir für heute Nacht reichlich "Arbeit" beschert. Kann sein, dass ich morgen früh nochmal nachfrage....
Gewinner des BCC #53 mit "Gitarrist vs Fussballer" http://www.midimaster.de/downl...ssball.exe

Midimaster

 BeitragFr, Jan 13, 2012 4:12
Antworten mit Zitat
Benutzer-Profile anzeigen
Einige Fragen zum Tutorial vom Darth....

Erst mal: Wahnsinn! Darth! Dass du gleich so ein Tutorial schreibst, hätte ich nicht erwartet. Es ist superhilfreich! Und das ganze auch noch mit BB-Code zeigt einem, wie man es auch in eine Programmiersprache umsetzt.

Doch einige Fragen habe ich noch. Da ich den Tutorial-Thread nicht "verschmutzen" wollte, stell ich sie hier und hoffe, du findest das hier:

Du schreibst...
Zitat:
Dann gibt es aber noch die Vektormultiplikation....

Kanst du mir auch hier eine praxisnahme Anwendungsmöglichkeit nennen? Was erfahre ich durch das Ergebnis. Was rauskommt scheint ja nun kein Vektor mehr zu sein, sondern einfach eine Zahl. Hast Du das in eigenen Programmen schon benötigt? Wenn ja, wobei?



Du schreibst...
Zitat:
2.2 Winkel zwischen Vektoren

Das Skalarprodukt zweier Vektoren ist der Cosinus des Winkels zwischen ihnen.
Code:
a = ACos(A * B)

Müßte es nicht "zweier normalisierter Vektoren" heißen. Weil durch das oben beschriebe Verfahren vdot() sind doch auch Ergebnisse über 1 zu erwarten. Ein COS() hat aber doch nur Ergebnisse zwischen 0 und 1, oder? Für einen Test auf rechter Winkel wäre es egal, aber für COS()?



Du schreibst...
Zitat:
Leider heisst das, dass man immer 2 Gleichungen behandeln muss

Sind das dann diese beiden?
Code: [AUSKLAPPEN]
Px = Ax + t * Gx
Py = Ay + t * Gy


oder meinst Du, dass man mit dem Ortsvektor zu A und den GeradenVektor G arbeiten muss?



Du schreibst...
Zitat:
R = V - 2 * N * (N * V)

Wie kommt man von sowas auf diese Umsetzung in BB:
BlitzBasic: [AUSKLAPPEN] 
	nl = vLength2D(n)
	dp = 2*vDot3D(v, n) /(nl *nl)
	r\x = v\x - dp *n\x
...

mir ist wieder mal schleierhaft, wie da die Zusammenhänge sind. Ich erkenne vielleicht noch das V wieder und die "2", aber wie kommst Du auf das "nl^2! oder auf das Geteilt-Zeichen? Hier steige ich wieder aus.

So, jetzt werde ich mir noch dein anderes Code-Beispiel reinziehen und danke auch für den tolle link zur Diplomarbeit. Da es um Schienen geht kann ich es gut brauchen.

oh. schon wieder 3:00 Uhr
Gewinner des BCC #53 mit "Gitarrist vs Fussballer" http://www.midimaster.de/downl...ssball.exe

darth

 BeitragFr, Jan 13, 2012 13:03
Antworten mit Zitat
Benutzer-Profile anzeigen
Hallo,

danke für die Anregungen. Ich habe es im Thread editiert (und dich zur Nachhilfeschülerin gemacht.. aber keine Angst, du hast grosse blaue Augen :>). Hier trotzdem nochmal kurz:

Die Vektormultiplikation/Skalarmultiplikation ist eingentlich eine Projektion des einen Vektors auf einen anderen. Aber da ich mich damit nicht aufhalten wollte (weil das Wort wahrscheinlich nur verwirrt) habe ich das weggelassen. Wofür man die Multiplikation brauchen kann, folgt ja in einem späteren Kapitel mit dem Winkel zwischen Vektoren.
Hierzu gleich auch ein Dankeschön. Natürlich müssen die Vektoren normalisiert sein, ist zwischen Edits wohl verlorengegangen, ist jetzt wieder eingefügt mit einer allgemeinen Form.

Bei den beiden Gleichungen hast du recht. Der Parameter t muss man (da skalare Multiplikation) auf jeden Vektorkomponenten einzeln anwenden, d.h du kriegst eine Gleichung für X und eine für Y. Das mag in manchen Fällen von Vorteil sein (Verschiebungen z.b, oder ausrechnen von UV Koordinaten), aber meist ist diese Form halt unhandlicher. Es ist eigentlich eine Gewohnheitsfrage, mir ist diese Form generell lieber, weil sie intuitiver ist.

Die Herleitung des Codes habe ich in einem kurzen Edit lang und breit erklärt (haha, Oxymoron!). Kurz gesagt: Das 1/n^2 kommt von der Normierung des N Vektors. Ich wollte beim Code nicht davon ausgehen, dass dieser schon normiert in die Funktion kommt (aus diversen Gründen), da die Formel aber nur für n = 1 korrekt ist, muss man die beiden N Vektoren noch normieren, d.h es kommt jeweils 1/n dazu, das zweimal und 1/n * 1/n = 1/n^2. Und woher die 2 und das Dotproduct kommt sollte eigentlich klar sein :/ das steht 1:1 so in der Formel.

Hoffe das klärt das meiste,
MfG,
Darth
Diese Signatur ist leer.

Midimaster

 BeitragSa, Jan 14, 2012 11:25
Antworten mit Zitat
Benutzer-Profile anzeigen
So langsam glaube ich lichten sich die Nebel in meinem Hirn. Der Hinweis auf die Projektion ist sogar sehr hilfreich dabei. Er scheint die zentrale Stelle in vielen Operationen mit Vektoren zu sein und erklärt so einiges.

Wenn ich das so richtig verstanden habe, dann passiert beim Vektor-Produkt folgendes:

user posted image

Der rote Vektor befindet sich im Welt-Koordinatensystem. Sein X- und Y-Anteil entspricht dem waagrechten und senkrechten Wertej im System.

Nach der KreuzVektor-Multiplikation mit dem grünen Vektor stellen seine X- und Y-Werte den Wert dar, den sie im "grünen Koordinatensystem" hätten. Es ist als ob das Koordinatensystem eine neue Ausrichtung hätte. Das erklärt auch warum man vom COS() spricht.

Was für den Laien glaube ich auch sehr verwirrend ist, ist die Tatsache dass man von normalisieren und vom Normal spricht und beides etwas völlig anderes bedeutet. Welches der beiden meinst du aber mit "normieren"?


So sehe ich es momentan:

Ein normalisierter Vektor zeigt in die Vektor-Richtung, hat aber die Länge 1. Seine x- und y-Komponenten sind quasi SIN() und COS() seiner Richtung.

Ein Normal zeigt 90° vom Vektor weg und hat ebenfalls die Länge 1. Es ist quasi die Senkrechte auf den Vektor.



Und jetzt nochmal zu deinem Absatz zur "Geradengleichung"

ich male mal die Zeichung selbst:

user posted image

Was genau meinst Du nun mit C? Ist das ein Wert? Eine Verschiebung auf y? Oder wieder eine Vektor mit 2 Komponenten?

Und was meinst du mit ...
Code: [AUSKLAPPEN]
...Und der Zauber wäre vollbracht...
? Was ist damit gewonnen?




Und hier noch ein Nachsatz zu der Reflektion, nur um sicher zu gehen, dass ich es verstanden habe. Du schreibst:
Zitat:
..."R = V - 2 * N * (N * V)"
".. Also machen wir das für sie!"
"R = V - 2 * N/n * (N/n * V)"


Dabei ist Dein N ein Vektor und n die Länge dieses Vektors. Das habe ich jetzt verstanden. Ist das allgemein so, dass in solchen Formeln kleine Buchstaben als "Länge" zu lesen sind?


So, nun zu deinem Code-Beispiel für mein Abstandsproblem (dein Post vom 12.1 17:20)
Hier erkenne ich nun immer mehr:

hier beschreibst Du die Geraden durch die "Geradengleichung":
BlitzBasic: [AUSKLAPPEN] 
	l = getLength(g1)
	
	n1 = getNormal(g1)
	c1 = -n1\x * m\x - n1\y * m\y
		;-> n1\x * X + n1\y * Y + c1 = 0 für alle Punkte auf g1
	
	;geradengleichung 2:
	n2 = getNormal(g2)
	c2 = -n2\x * m\x - n2\y * m\y
Klar!

aber hier wird eswieder undurchsichtig für mich:
BlitzBasic: [AUSKLAPPEN] 
	;Gleichung 1:
	;	(n1\x * t\x + n1\y * t\y + c1) / l = d < HNF
	;Gleichung 2:
	;	n2\x * t\x + n2\y * t\y + c2 = 0 < Pt auf G2
	
	;2 Gleichungen
	;2 Unbekannte

wo kommt jetzt wieder das t her?

Ich danke Dir für Deine Geduld!!!


[EDIT]:
Nachtrag. Stimmen meine Gedanken zur Geradengleichung hier so?
Code: [AUSKLAPPEN]
gegeben sein Gerade G durch P

Gerade Vektor dazu: [Gx; GY]
Punkt P Ortsvektor: [Px;Py]

[A;B] NormalVekotr zu G also genau [Gy;-Gx]

Geradengleichung allgemein:
A*x + B*Y + C = 0

lässt sich dann daraus dies folgern:
Gy*PX + -Gx*PY + C = 0



Nochmal zur HNF:

Zitat:
;Gleichung 1:
; (n1\x * t\x + n1\y * t\y + c1) / l = d < HNF

ich glaub, ich weiß jetzt was das T soll: [tx;ty] wird der Punkt auf der Geraden G", der genau den Abstand 50 zur G1 hat?

Zitat:
;aufgelöst nach t\x und t\y
det# = n1\x * n2\y - n1\y * n2\x

das versteh ich nicht? Welche der beiden Gleichungen hast du da da wie aufgelöst um zu diesem Ergebnis zu kommen? Das ist doch ein Vektorprodukt aus den Normalen der beiden Geraden, oder? Das kam ja so auch bei deinem Abschnitt über Refketion vor. Aber was hat es hiermit zu tun?
Gewinner des BCC #53 mit "Gitarrist vs Fussballer" http://www.midimaster.de/downl...ssball.exe

darth

 BeitragSa, Jan 14, 2012 14:03
Antworten mit Zitat
Benutzer-Profile anzeigen
Hallo,

na du hast ja mal wieder viele Fragen..

Das mit dem Vektorprodukt hast du im grossen so richtig gesehen. Nur der Satz
Zitat:
Nach der KreuzVektor-Multiplikation mit dem grünen Vektor

verwirrt mich grad. Kreuzprodukt geht NUR in 3D. Das ist eine definierte Rechenregel für 3 Komponenten. In 2D gibt es das nicht.

Zum Skalarprodukt vllt noch dies: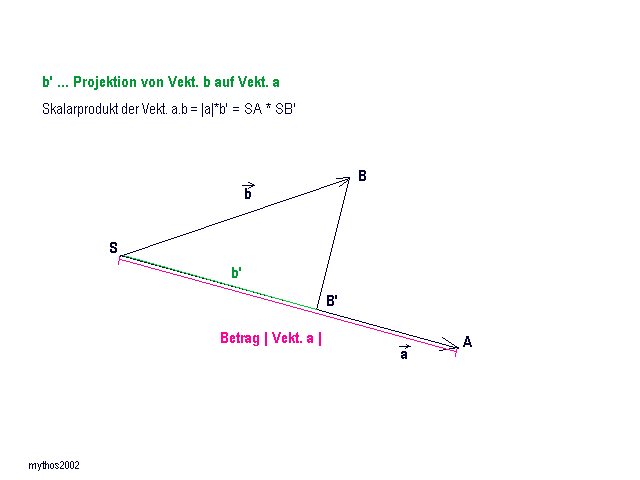
user posted image

Wie du siehst ist die Projektion dann b' (Länge, nicht Vektor). Das gibt wieder ein rechtwinkliges Dreieck, und daher kommt der Cosinus (Ankathete b' über Hypothenuse b).

Die Verwirrung mit normalisieren und Normale ist mir bewusst, aber da gibt es keinen Weg darum. Kommt wohl davon, dass man die Normale meist normiert, weil da nur die Richtung eine Rolle spielt.
Normieren heisst auf Länge 1 bringen.

Code: [AUSKLAPPEN]
Ein normalisierter Vektor zeigt in die Vektor-Richtung, hat aber die Länge 1. Seine x- und y-Komponenten sind quasi SIN() und COS() seiner Richtung.


Jup. Kommt vom Einheitskreis, und der Tatsache, dass sin^2 + cos^2 = 1.

user posted image

C ist ein Wert. Wenn du so willst kannst dus als Verschiebung auf der y-Achse ansehen. Eine Funktionsgleichung f(x) hat ja eine ähnliche Form:
y = f(x) = m * x + q
Wenn du jetzt die Geradengleichung A*x + B*y + C = 0 anschaust, kannst du das nach y auflösen (Arithmetik):
y = -A/B * x - C/B
Es ist also nicht genau die Verschiebung auf der y-Achse, sondern die Verschiebung des Vektors zu dem bestimmten Punkt. Ich kann jetzt hier nicht P sagen, weil in deinem Bild P nicht auf der Geraden liegt. Der Punkt wäre dort, wo sich deine grüne Linie D mit der roten g schneidet.

Zitat:
...Und der Zauber wäre vollbracht...

Heisst i.A. dass man fertig ist mit der Rechnung/Aufgabe. Ich weiss grad nicht woher du das hast, darum kann ich nciht wirklich antworten.

Ja, N ist Vektor, n ist Länge. Normalerweise hat man N(mit Vektorpfeil) und N (weil man generell Kleinbuchstaben nimmt). Aber da ich keine Vektorpfeile setzen kann, sind Grossbuchstaben Vektoren und Kleinbuchstaben ihre Längen.

Dieses T ist der Schnittpunkt den du haben willst.

Deine Überlegungen zu den Geradengleichungen sind richtig.

Schreib dir mal beide Gleichungen übereinander auf und lös sie nach Tx und Ty auf. Du wirst sehen, dass du diesen "Bruch" den ich im Code als det# bezeichnet habe bei beiden Resultaten stehen wird. Das kommt daher, dass man die Gleichung in eine Matrix schreiben könnte (also A * t = b) und dann mit Wissen aus der linearen Algebra sagen kann, wie die Inverse von A aussehen wird.
Code: [AUSKLAPPEN]
A^-1 * A * t = I * t = t = A^-1 * b

Oder du schnappst dir beide Gleichungen und bentutzt ein Mathematik-Programm wie Mathematica/WolframAlpha um auf die Resultate zu kommen.

PS: Es ist NICHT ein Vektorprodukt, weil da eine - steht und kein +. Wenn mans genau nimmt wäre es der Z-Eintrag des Kreuzproduktes von [N1x ; N1y ; 0] x [N2x ; N2y ; 0], aber woher es kommt ist eigentlich egal, es ist wirklich einfach nur das Auflösen der beiden Gleichungen. (Schulmathematik 5. Primarstufe oder so.. Gleichungen lösen).

MfG,
Darth
Diese Signatur ist leer.

Midimaster

 BeitragMo, Jan 16, 2012 20:30
Antworten mit Zitat
Benutzer-Profile anzeigen
Hallo Darth,

ich hab jetzt mich mal zwei Modifikationen an Deinem Code getraut:

zum einem habe ich den Ortsvektor M [400;300] aus der Berechnung entfernt, weil ich ja den "endgültigen" Punkt P auch durch eine Vektoraddition mit M zum Schluss erhalten kann.

zum anderen habe ich statt der Vektoren G1 und G2 die normalisierten Vektoren verwendet. Damit ist C1 und C2 immer Null. Und jetzt fällt total viel aus den Formeln raus:
BlitzBasic: [AUSKLAPPEN] 
Type Vector2
	Field x#
	Field y#
End Type

Function newVector.Vector2(x#, y#)
	Local v.Vector2 = New Vector2
	v\x = x
	v\y = y
	Return v
End Function

Function getNormal.Vector2(v.Vector2)
	Return newVector(v\y, -v\x)
End Function

Function getLength#(v.Vector2)
	Return Sqr(v\x * v\x + v\y * v\y)
End Function



Graphics 800, 600, 0, 2
SetBuffer BackBuffer()

Local m.Vector2
Local g1.Vector2
Local g2.Vector2
Local d#

m = newVector(400, 300)
g1 = newVector(4, 1)
g2 = newVector(3, -1)

d = 50

Local l#, t.Vector2

; neu: Vorbereitung G1 normalisieren
L=getLength(g1)
g1\x = g1\x/l
g1\y = g1\y/l

; neu: Vorbereitung G2 normalisieren
L=getLength(g2)
g2\x = g2\x/l
g2\y = g2\y/l



While Not KeyHit(1)
	
	Oval m\x -3, m\y -3, 6, 6
	Line m\x + 1000 * g1\x, m\y + 1000 * g1\y, m\x - 1000 * g1\x, m\y - 1000 * g1\y
	Line m\x + 1000 * g2\x, m\y + 1000 * g2\y, m\x - 1000 * g2\x, m\y - 1000 * g2\y

	g2\x=g2\x-.01
	
;grass: auch das führt zum Ergebnis:
	det# = g1\x * g2\y - g1\y * g2\x

	t = New Vector2
	t\x = -(d  * g2\x ) /det
	t\y = -(d * g2\y ) /det
	
	;Resultat
	Oval m\x +t\x -49, m\y +t\y -49, 100, 100,0
	Oval m\x +t\x -4, m\y +t\y -4, 7, 7,0
	
	Flip
	Cls
Wend
End

... und funktioniert aber immer noch! Ist das noch legal, oder habe ich einen Denkfehler und es wird jetzt zu Problemen kommen?
Gewinner des BCC #53 mit "Gitarrist vs Fussballer" http://www.midimaster.de/downl...ssball.exe

darth

 BeitragMo, Jan 16, 2012 22:09
Antworten mit Zitat
Benutzer-Profile anzeigen
Hallo,

du hast recht. Es ist eigentlich egal, wo ich die Verschiebung durchführe. Ich kann mein neues Koordinatensytem durch M legen, so dass beide Geraden durch den (neuen) Ursprung gehen, dann fallen die Cs weg. Und nachher wieder zurück schieben.

Zitat:
... und funktioniert aber immer noch! Ist das noch legal, oder habe ich einen Denkfehler und es wird jetzt zu Problemen kommen?


Wenns funktioniert, und nicht nur für einen bestimmten Sonderfall, dann ists doch in Ordnung? Ich habs jetzt nicht ganz nachgerechnet, aber mir scheint, dass durch die Definition der Normalen viele Dinge wegzufallen scheinen (die Cs sind klar). Siehe z.b die Variable det. Aber so auf einen Blick scheint es richtig zu sein.

Die Normierung von g2 kannst du dir eigentlich auch sparen - machst du im Prinzip ja auch. Du veränderst g2 in deinem Code in jedem Durchlauf, führst die Normierung aber nur einmal vor der Schleife durch. Aber ehrlich gesagt bin ich mir selber nicht ganz sicher, wieso man das nicht braucht. Muss wahrscheinlich in irgend einer Zwischenrechnung mal rausfallen. G1 musst du allerdings normieren, sonst fällts auseinander.

Meiner Meinung nach ist es etwas "unschön" wie du T definierst, ich würde die Vektoraddition mit M direkt ins T reinschreiben, nicht erst beim Zeichnen des Ovals - aber das ist wohl Geschmackssache. Für mich ist T halt das Endresultat, bei dir ist es "nur" ein Zwischenschritt.

Kleine Anmerkung noch (rein Codetechnisch): Du erstellst in jedem Schleifendurchlauf ein neues T und entfernst es nicht. D.h irgendwann wird dein Speicher überlaufen. Aber da dies nur ein kleiner Testcode ist, kann ein solcher Flüchtigkeitsfehler schnell einmal auftauchen, sollte einfach entfernt werden, wenn du das dann in irgend ein richtiges Spiel übernehmen willst. Solche Mem-Leaks sind nervig zu finden Smile

MfG,
Darth
Diese Signatur ist leer.

Midimaster

 BeitragMo, Jan 16, 2012 23:21
Antworten mit Zitat
Benutzer-Profile anzeigen
Wahnsinn, oder? Wie klar das plötzlich aussieht.... So ähnlich dachte ich mir, dass es werden müßte, wenn man Vektoren statt SIN(), COS() verwendet. Aber gleich so klar? Wow!

Dass die Normalisierung von G2 nicht in der Schleife erfolgte war ein Tippfehler von mir. Und nun bin ich auch sehr überrascht, dass das funktioniert. Da werde ich noch mal darüber nachdenken müssen...

Ich benötige den Vektor t wahrscheinlich im späteren Programm immer nur als Vektor von M hin zum Punkt T. Daher erfolgt keine absoulte Berechnung. M kann durch den User verschoben werden, T muss dann sowieso ausgerechnet werden. Außerdem gibt es im Spiel später zu jedem M vier T's.

Der Tipp mit dem Lifecycle der TYPEN innerhalb von Funktionen ist wieder mal Gold wert. Daran hätte ich sicher nicht mehr gedacht. In BMAX sind ja auch "locale custom types" wirklich tot nach Verlassen der Funktion, in BB aber muss ich daran denken! Da da TRAM-Spiel in B3D entsteht muss ich mich echt umgewöhnen. (Hier im Testprogramm spielt es ja keine Rolle)

So, dann werde ich alle Erkenntnisse in den neuen Straßenalgo einbauen. Irgendwann gibt es dann auch einen Screenshot oder sogar den Algo hier.

Nochmals vielen Dank Dir! Das war schon mehr Hilfe als man erwarten konnte. Ich hab auch was gelernt dabei. Ich hoffe, ich kann das irgenwann mal dem Forum wiedergutmachen, was ich hier so alles an Hilfe erhalte!
Gewinner des BCC #53 mit "Gitarrist vs Fussballer" http://www.midimaster.de/downl...ssball.exe

Neue Antwort erstellen


Übersicht BlitzBasic Allgemein

Nach Oben

Gehe zu:

Powered by phpBB © 2001 - 2006, phpBB Group